
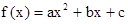 满足:
满足: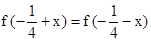 ,且
,且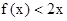 的
的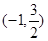
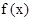 的解析式;
的解析式;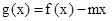
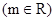 ,若
,若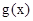 在
在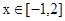 上的最小值为-4,求
上的最小值为-4,求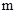 的值.
的值.
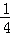 对称,得到a=2b,再由f(x)<2x的解集为
对称,得到a=2b,再由f(x)<2x的解集为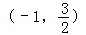 得到相应方程的根为x1=﹣1,x2=
得到相应方程的根为x1=﹣1,x2=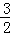 且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;
且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;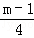 对称.因此分m<﹣3时、﹣3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.
对称.因此分m<﹣3时、﹣3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.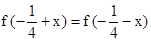 ∴
∴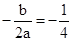 即
即 ①
① 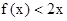 即
即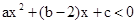 的解集为
的解集为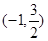
 是
是 的两根且a>0.
的两根且a>0. 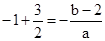 ②
②  ③
③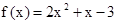
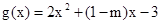 其对称轴方程为
其对称轴方程为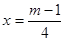
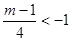 即m<-3时,
即m<-3时,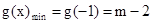
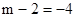 得
得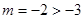 不符合题意
不符合题意 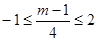 即
即 时,
时, ,
,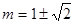 符合
符合
 即m>9时,
即m>9时,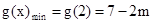
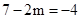 得
得 不符合题意
不符合题意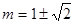


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:单选题
| A.f(1)+2f(1)+3f(1)+…+nf(1) | B.f[
| ||
| C.n(n+1) | D.n(n+1)f(1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
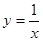 (x>0)图像上一动点,若点P,A之间的最短距离为
(x>0)图像上一动点,若点P,A之间的最短距离为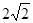 ,则满足条件的实数a所有值为_________.
,则满足条件的实数a所有值为_________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
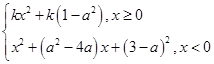 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com