Question

17．已知E、F、G、H分别是空间四边形ABCD各边AB、AD、CB、CD上的点，并且有$\frac{AE}{EB}$=$\frac{CG}{GB}$，$\frac{AF}{FD}$=$\frac{CH}{HD}$，试证EF、GH、BD共点或两两平行．

Answer 1

分析 证明E、F、H、G四点共面于α，于是EF与HG只有相交与平行两种可能，分类讨论，利用公理2，4，即可得出结论．

解答 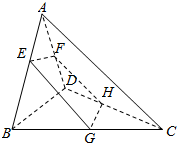证明：如图，连AC、EG、FH，在△ABC中，
∵$\frac{AE}{EB}$=$\frac{CG}{GB}$，∴EG∥AC．同理FH∥AC，于是根据公理4可知：EG∥FH．
∴E、F、H、G四点共面于α，于是EF与HG只有相交与平行两种可能．
（Ⅰ）若EF与HG相交，设交点为P，则P∈EF，EF⊆平面ABD．
∴P∈平面ACD，
同理可知：P∈平面BCD．∴P是平面ABD与平面BCD的公共点．
∴两平面的交线BD必过P点．∴FE、GH、BD共点．
（Ⅱ）若EF与HG平行，则必有EF∥BD．∵EF∥平面ABD、BD∥平面ABD，
∴若EF与BD不平行，则EF与BD就相交，设交点为Q，则EF⊆平面EFHG，Q∈BD，BD⊆平面BDC，
∴Q是平面EFHG与平面BDC的公共点．
又∵HG是这两个平面的交线，∴Q∈HG，
∴EF∩HG=Q．这就与EF∥HG相矛盾，故假设错误．
∴EF∥BD．同理可证：HG∥BD．故由公理4知：EF、HG、BD两两平行．

点评 本题考查直线与直线，平面与平面的位置关系，考查平面的基本性质，考查学生分析解决问题的能力，属于中档题．