
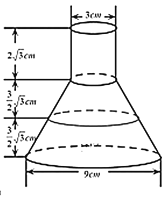
【题目】《乌鸦喝水》是《伊索寓言》中一个寓言故事,通过讲述已知乌鸦喝水的故事,告诉人们遇到困难要运用智慧,认真思考才能让问题迎刃而解的道理,如图![]() 所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为
所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为![]() 厘米,瓶底直径为
厘米,瓶底直径为![]() 厘米,瓶口距瓶颈为
厘米,瓶口距瓶颈为![]() 厘米,瓶颈到水位线距离和水位线到瓶底距离均为
厘米,瓶颈到水位线距离和水位线到瓶底距离均为![]() 厘米,现将
厘米,现将![]() 颗石子投入瓶中,发现水位线上移
颗石子投入瓶中,发现水位线上移![]() 厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
A.![]() 颗B.
颗B.![]() 颗C.
颗C.![]() 颗D.
颗D.![]() 颗
颗
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为![]() 吨,最多为
吨,最多为![]() 吨,月处理成本
吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为
,且每处理一吨二氧化碳得到可利用的化工产品价值为![]() 元.
元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
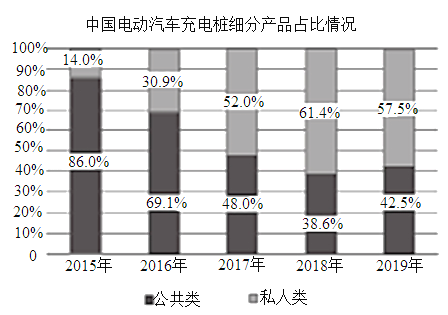
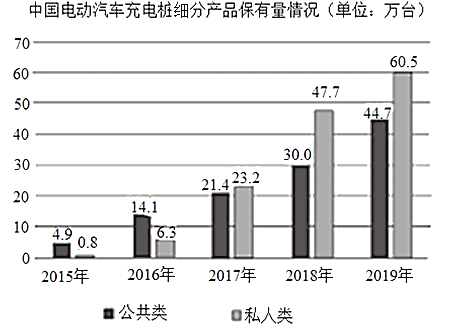
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 是某生态农庄的一块植物栽培基地的平面图,现欲修一条笔直的小路
是某生态农庄的一块植物栽培基地的平面图,现欲修一条笔直的小路![]() (宽度不计)经过该矩形区域,其中
(宽度不计)经过该矩形区域,其中![]() 都在矩形
都在矩形![]() 的边界上.已知
的边界上.已知![]() ,
,![]() (单位:百米),小路
(单位:百米),小路![]() 将矩形
将矩形![]() 分成面积分别为
分成面积分别为![]() ,
,![]() (单位:平方百米)的两部分,其中
(单位:平方百米)的两部分,其中![]() ,且点
,且点![]() 在面积为
在面积为![]() 的区域内,记小路
的区域内,记小路![]() 的长为
的长为![]() 百米.
百米.
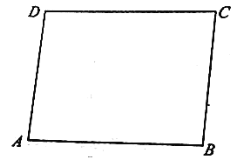
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是__________.
①平均数![]() ; ②标准差
; ②标准差![]() ; ③平均数
; ③平均数![]() 且标准差
且标准差![]() ;
;
④平均数![]() 且极差小于或等于2; ⑤众数等于1且极差小于或等于4.
且极差小于或等于2; ⑤众数等于1且极差小于或等于4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥VABCD中,底面ABCD是矩形,VD⊥平面ABCD,过AD的平面分别与VB,VC交于点M,N.

(1) 求证:BC⊥平面VCD;
(2) 求证:AD∥MN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com