
平面直角坐标系 中,过椭圆
中,过椭圆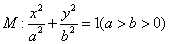 右焦点的直线
右焦点的直线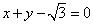 交
交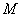 于
于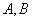 两点,
两点,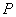 为
为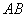 的中点,且
的中点,且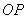 的斜率为
的斜率为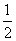 .
.
(Ⅰ)求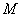 的方程;
的方程;
(Ⅱ)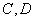 为
为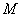 上的两点,若四边形
上的两点,若四边形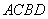 的对角线
的对角线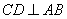 ,求四边形ACBD面积的最大值.
,求四边形ACBD面积的最大值.
解 (Ⅰ)设A (x 1, y 1) ,B (x 2, y 2),P (x 0, y 0)
⇒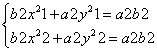 ⇒
⇒ 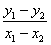 =
= 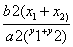 ⇒ kAB =
⇒ kAB = 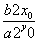
OP的斜率为 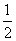 ⇒
⇒  = 2,直线x + y
= 2,直线x + y 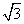 = 0的斜率为1 ⇒ kAB =1
= 0的斜率为1 ⇒ kAB =1
⇒1= 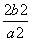 ⇒ a2 = 2b2 ……①
⇒ a2 = 2b2 ……①
由题意知直线x + y 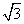 = 0与x轴的交点F(
= 0与x轴的交点F(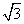 ,0)是椭圆的右焦点,则才c =
,0)是椭圆的右焦点,则才c = 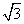
⇒a2 b2 = 3 ……②
联立解得①、②解得a2 = 6,b2 = 3
所以M的方程为: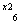 +
+ 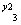 = 1
= 1
(Ⅱ)联立方程组 ,解得A(
,解得A(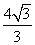 ,
, 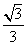 )、B(0,
)、B(0, 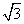 ),求得| AB | =
),求得| AB | = 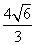
依题意可设直线CD的方程为:y = x + m
CD与线段AB相交⇒ 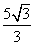 < m <
< m < 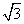
联立方程组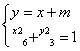 消去x得:3x 2 + 4mx +2m2 6 = 0 …… (*)
消去x得:3x 2 + 4mx +2m2 6 = 0 …… (*)
设C (x 3, y 3),D (x 4, y 4),则| CD |2 = 2(x 3 x 4)2 = 2[(x 3 + x 4)2 4x 3x 4]= 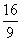 (9 m2)
(9 m2)
四边形ACBD的面积S = 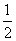 | AB |• | CD | =
| AB |• | CD | = 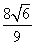
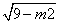
当n = 0时,S最大,最大值为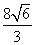 .
.
所以四边形ACBD的面积最大值为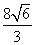 .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
若数列{an}是等比数列,则数列{an+an+1} ( )
A.一定是等比数列
B.可能是等比数列,也可能是等差数列
C.一定是等差数列
D.一定不是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
已知l,m,n是三条不同的直线,α,β是不同的平面,则下列条件中能推出α⊥β的是
A.l α,m
α,m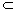 β,且l⊥m B.l
β,且l⊥m B.l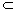 α,m
α,m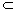 β,n
β,n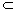 β,且l⊥m,l⊥n
β,且l⊥m,l⊥n
C.m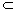 α,n
α,n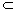 β,m//n,且l⊥m D.l
β,m//n,且l⊥m D.l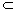 α,l//m,且m⊥β
α,l//m,且m⊥β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com