练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知A＝{y|y＝log2x，x＜1}，B＝{y|y＝()x，x＞1，则A∩B＝

    [　　]

    A．

    B．(－∞，0)

    C．(0，)

    D．(－∞，)

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知抛物线C1：y＝x2＋2x和C2：＝－x2＋a．如果直线l同时是C1和C2的切线，称l是C1和C2的公切线，公切线上两个切点之间的线段，称为公切线段．

    (Ⅰ)a取什么值时，C1和C2有且仅有一条公切线？写出此公切线的方程；

    (Ⅱ)若C1和C2有两条公切线，证明相应的两条公切线段互相平分．

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学理科(广东B卷) 题型：044

    已知曲线C：y＝x2与直线l：x－y＋2＝0交于两点A(xA，yA)和B(xB，yB)，且xA＜xB．记曲线C在点A和点B之间那一段L与线段AB所围成的平面区域(含边界)为D．设点P(s，t)是L上的任一点，且点P与点A和点B均不重合．

    (1)若点Q是线段AB的中点，试求线段PQ的中点M的轨迹方程；

    (2)若曲线与点D有公共点，试求a的最小值．

    查看答案和解析>>

    科目：高中数学 来源：辽宁省锦州中学2012届高三上学期第一次月考数学理科试题 题型：044

    已知A，B，C是直线l上的不同的三点，O是外一点，向量，，满足：－(x2＋1)·－[ln(2＋3x)－y]·＝0．记y＝f(x)．

    (1)求函数y＝f(x)的解析式；

    (2)若对任意x∈[，]，不等式|a－lnx|－ln[(x)－3x]＞0恒成立，求实数a的取值范围；

    (3)若关于x的方程f(x)＝2x＋b在[0，1]上恰有两个不同的实根，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：浙江省瑞安市十校2012届高三上学期期中联考数学理科试题 题型：044

    如图，已知直线l：y＝2x＋m(m＜0)与抛物线C1：y＝ax2(a＞0)和圆C2：x2＋(y＋1)2＝5都相切，F是C1的焦点．

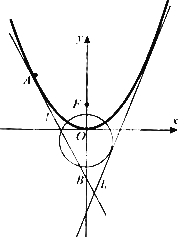
    (1)求m与a的值；

    (2)设A是C1上的一动点，以A为切点作抛物线C1的切线l，直线l交y轴于点B，以FA，FB为邻边作平行四边形FAMB，证明：点M在一条定直线上；

    (3)在(2)的条件下，记点M所在的定直线为l2，直线l2与y轴交点为N，连接MF交抛物线C1于P，Q两点，求△NPQ的面积S的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知椭圆＝1(a＞b＞0)过点(1，)，离心率为，左、右焦点分别为F1、F2.点P为直线l：x＋y＝2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．

    (1)求椭圆的标准方程．

    (2)设直线PF1、PF2的斜率分别为k1、k2.

    (ⅰ)证明：＝2.

    (ⅱ)问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA＋kOB＋kOC＋kOD＝0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案