
 平移得到直线l,N为l上的动点,M为抛物线弧AB上的动点.
平移得到直线l,N为l上的动点,M为抛物线弧AB上的动点. 的最小值.
的最小值.
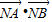 的最小值.
的最小值.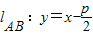 ,则
,则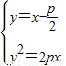 ,消去x得:
,消去x得: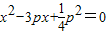 ①,则x1+x2=3p,
①,则x1+x2=3p,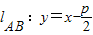 ,设
,设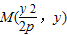 ,
,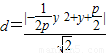 ,因M,O在直线AB的同侧,所以
,因M,O在直线AB的同侧,所以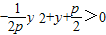 ,
,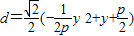 ,即
,即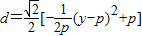 ,
,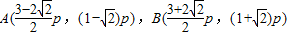
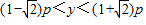 ,则当y=p时,
,则当y=p时,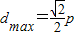 ,
,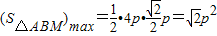 .---------------------------------------(8分)
.---------------------------------------(8分)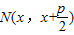 ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),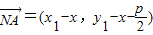 ,
,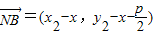 ,
,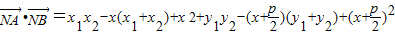
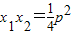 ,
,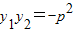 ,y1+y2=2p,则
,y1+y2=2p,则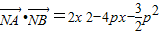 ,
,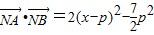 ,当x=p时,
,当x=p时,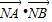 的最小值为
的最小值为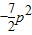 .
.

科目:高中数学 来源: 题型:
 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量| a |
| NA |
| NB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量| a |
| NA |
| NB |
查看答案和解析>>
科目:高中数学 来源:山东省枣庄市2010届高三年级调研考试数学(文科)试题 题型:解答题
(本题满分12分)
如图,斜率为1的直线 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com