A
分析:由题意知此题为恒成立问题,要求?x∈[0,+∞)都有f(x)≥g(x),首先构造函数H(x)=f(x)-g(x),利用导数求H(x)在[0,+∞)上的最小值,因为两个极值点大小没法判断,于是要进行分类讨论,所求最小值含有a,只要令H
min(x)>0,解出a的范围即可.
解答:构造函数H(x)=f(x)-g(x)=x
3+(2-a)x
2+4,
只要证明H(x)在[0,+∞)上的最小值大于等于0即可;
H′(x)=3x
2+2(2-a)x=x(3x+4-2a),令H′(x)=0得,
x
1=0,x
2=
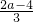
,
①若a>2时,x
2>0;当0<x<x
2时,H′(x)<0,H(x)为减函数;
当x>x
2时,H′(x)>0,H(x)为增函数;
H(x)在x=x
2处取极小值,也是最小值,H
min(x
2)=H(
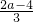
)=
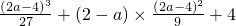
,
令H
min(x
2)≥0,解得a≤5,综上2<a≤5;
②若a≤2时,x
2<0;当x≥0时,H′(x)>0,H(x)为增函数;
H(x)在x=0处取极小值,也是最小值,H
min(x
2)=H(0)=4>0,恒成立;
∴a≤2,
综上①②得a≤5.
故选A.
点评:解此题的关键是构造函数H(x),将恒成立问题转化为函数求导求最值问题,是解此题的一般思路,另外此题还用到分类讨论的思想.



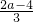 ,
,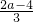 )=
)=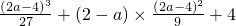 ,
,

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<