练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列叙述错误的是（ ）．

    A.若事件发生的概率为，则

    B.互斥事件不一定是对立事件，但是对立事件一定是互斥事件

    C.某事件发生的概率是随着试验次数的变化而变化的

    D.5张奖券中有一张有奖，甲先抽，乙后抽，则乙与甲中奖的可能性相同

    【答案】C

    【解析】

    根据必然事件，不可能事件，随机事件的概念判断选项A正确；根据对立事件是互斥事件的子集判定选项B正确；根据概率具有确定性，是不依赖于试验次数的理论值判断C错误；根据抽签有先后，对每位抽签者是公平的判断D正确.

    根据概率的定义可得若事件发生的概率为，则，故A正确；

    根据互斥事件和对立事件的定义可得，互斥事件不一定是对立事件，但是对立事件一定是互斥事件，

    且两个对立事件的概率之和为1，故B正确；

    某事件发生的概率不会随着试验次数的变化而变化，故C错误；

    5张奖券中有一张有奖，先抽，后抽中奖的可能性相同，与次序无关，故D正确，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知A是圆O：x2+y2＝4上一动点，过点A作AB⊥x轴，垂足为B，动点D满足.

    （1）求动点D的轨迹C的方程；

    （2）垂直于x轴的直线M交轨迹C于M、N两点，点P（3，0），直线PM与轨迹C的另一个交点为Q.问：直线NQ是否过一定点？若过定点，求出该定点的坐标；若不过定点，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列判断正确的是（ ）

    A.“”是“”的充分不必要条件

    B.函数的最小值为2

    C.当时，命题“若，则”为真命题

    D.命题“，”的否定是“，”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校共有名学生，其中男生人，为了解该校学生在学校的月消费情况，采取分层抽样随机抽取了名学生进行调查，月消费金额分布在之间．根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示：

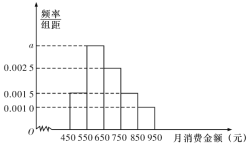
    将月消费金额不低于元的学生称为“高消费群”．

    （1）求的值，并估计该校学生月消费金额的平均数（同一组中的数据用该组区间的中点值作代表）；

    （2）现采用分层抽样的方式从月消费金额落在，内的两组学生中抽取人，再从这人中随机抽取人，记被抽取的名学生中属于“高消费群”的学生人数为随机变量，求的分布列及数学期望；

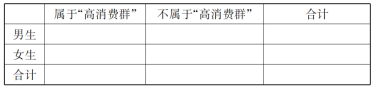
    （3）若样本中属于“高消费群”的女生有人，完成下列列联表，并判断是否有的把握认为该校学生属于“高消费群”与“性别”有关？

    （参考公式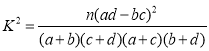：，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为(t为参数)，曲线C的极坐标方程为.

    （1）求直线l的普通方程和曲线C的直角坐标方程；

    （2）直线l与曲线C交于AB两点,P(1,3)，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中，底面ABC，，E，F分别为棱PB，PC的中点，过E，F的平面分别与棱AB，AC相交于点D，G，给出以下四个结论：

    ①；②；③；④.

    则以上正确结论的个数是

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    极坐标系中， 为极点，半径为2的圆的圆心坐标为.

    （1）求圆的极坐标方程；

    （2）设直角坐标系的原点与极点重合， 轴非负关轴与极轴重合，直线的参数方程为（为参数），由直线上的点向圆引切线，求切线长的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且椭圆C过点．

    (1)求椭圆C的标准方程；

    (2)过椭圆C的右焦点的直线l与椭圆C交于A、B两点，且与圆：交于E、F两点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在xOy中，曲线的参数方程为（t为参数）.在以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，曲线：，曲线：，.

    （1）把的参数方程化为极坐标方程；

    （2）设分别交，于点P，Q，求的面积.

    查看答案和解析>>

    同步练习册答案