
【题目】已知直线l的参数方程为![]() (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)直线l与曲线C交于AB两点,P(1,3),求![]() 的值.
的值.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点M ,使得![]() 恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( ).
A.若事件![]() 发生的概率为
发生的概率为![]() ,则
,则![]()
B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件
C.某事件发生的概率是随着试验次数的变化而变化的
D.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高的(不超过三次)多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
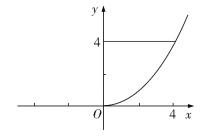
,![]() 依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线
依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
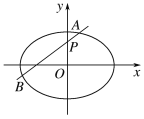
【题目】如图,椭圆E:![]() +
+![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2![]() .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得![]() =
=![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com