
【题目】在xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数).在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
(t为参数).在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]()
![]() ,
,![]() .
.
(1)把![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)设![]() 分别交
分别交![]() ,
,![]() 于点P,Q,求
于点P,Q,求![]() 的面积.
的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( ).
A.若事件![]() 发生的概率为
发生的概率为![]() ,则
,则![]()
B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件
C.某事件发生的概率是随着试验次数的变化而变化的
D.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同
查看答案和解析>>
科目:高中数学 来源: 题型:
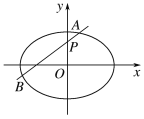
【题目】如图,椭圆E:![]() +
+![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2![]() .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得![]() =
=![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着甜品的不断创新,现在的甜品无论是造型还是口感都十分诱人,有颜值、有口味、有趣味的产品更容易得到甜品爱好者的喜欢,创新已经成为烘焙作品的衡量标准.某“网红”甜品店生产有几种甜品,由于口味独特,受到越来越多人的喜爱,好多外地的游客专门到该甜品店来品尝“打卡”,已知该甜品店同一种甜品售价相同,该店为了了解每个种类的甜品销售情况,专门收集了该店这个月里五种“网红甜品”的销售情况,统计后得如下表格:
甜品种类 | A甜品 | B甜品 | C甜品 | D甜品 | E甜品 |
销售总额(万元) | 10 | 5 | 20 | 20 | 12 |
销售额(千份) | 5 | 2 | 10 | 5 | 8 |
利润率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 |
(利润率是指:一份甜品的销售价格减去成本得到的利润与该甜品的销售价格的比值.)
(1)从该甜品店本月卖出的甜品中随机选一份,求这份甜品的利润率高于0.2的概率;
(2)假设每类甜品利润率不变,销售一份A甜品获利![]() 元,销售一份B甜品获利
元,销售一份B甜品获利![]() 元,…,销售一份E甜品获利
元,…,销售一份E甜品获利![]() 元,设
元,设![]() ,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过
,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com