
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用点在椭圆上及相切关系布列方程组,即可解得椭圆![]() 的标准方程;
的标准方程;
(2)联立方程易得: ![]() ,
, ![]() ,以
,以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,∴
轴正半轴上的顶点,∴![]() ,即
,即![]() 或
或![]() ,经检验得到结果.
,经检验得到结果.
试题解析:
法一(Ⅰ)由题意设椭圆的标准方程为![]() (
(![]() ,
, ![]() 且
且![]() )
)
∵![]() 在椭圆上,∴
在椭圆上,∴![]() ①
①
由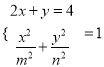 得
得![]()
∵椭圆![]() 与直线
与直线![]() 相切,∴
相切,∴![]() ,
,
即![]() ②
②
由①②知![]() ,
, ![]()
故所求椭圆方程为![]()
法二:设椭圆为![]() (
(![]() ,
, ![]() 且
且![]() )则它在点
)则它在点![]() 处的切线为
处的切线为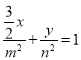 ,它与
,它与![]() 表示同一直线,∴
表示同一直线,∴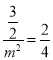 ,
, ![]() ,∴
,∴![]() ,
, ![]()
故所求椭圆方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() ,联立
,联立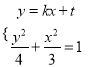
得![]()
![]() 得
得![]()
![]() ,
, ![]()
![]() ,
,
因为以![]() 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点![]()
∴![]() 即
即![]()
∴![]()
即![]()
即![]()
即![]()
∴![]() 或
或![]()
当![]() 时,直线
时,直线![]() 过定点
过定点![]() 与已知矛盾
与已知矛盾
当![]() 时,直线
时,直线![]() 过定点
过定点![]() 满足
满足![]()
所以,直线![]() 过定点,定点坐标为
过定点,定点坐标为![]()


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】正方体ABCD - A1B1C1D1的棱长为2, E、F、G分别为BC、CC1、BB1的中点,则( )
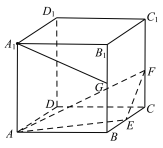
A.直线![]() 与直线AF垂直B.直线A1G与平面AEF平行
与直线AF垂直B.直线A1G与平面AEF平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点C与点G到平面AEF的距离相等
D.点C与点G到平面AEF的距离相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的标准参数方程;
的标准参数方程;
(2)求![]() 的长;
的长;
(3)以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,设点
轴的正半轴为极轴建立极坐标系,设点![]() 的极坐标为
的极坐标为![]() ;求点
;求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司计划在2010年向某企业投入800万元用于开发新产品,并在今后若干年内,每年的投入资金都比上一年减少20%.估计2010年可获得投资回报收入400万元,由于该项投资前景广阔,预计今后的投资回报收入每年都会比上一年增加25%.
(Ⅰ)设第![]() 年(2010年为第一年)的投入资金为
年(2010年为第一年)的投入资金为![]() 万元,投资回报收入为
万元,投资回报收入为![]() 万元,求
万元,求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)从哪一年开始,该投资公司前几年的投资回报总收入将超过总投入?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com