
| A�� | 1-$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$-$\sqrt{2}$ | B�� | 1+$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$+$\sqrt{2}$ | C�� | 1-$\sqrt{2}$��1+$\sqrt{2}$ | D�� | 2-$\sqrt{2}$��2+$\sqrt{2}$ |
���� ���ں���y=sin$\frac{��}{3}$x��AB����Ϊy=$\frac{\sqrt{3}}{2}$�������Ǻ���ͼ��������������Խ��Ʒ�ֵΪ1-$\frac{\sqrt{3}}{2}$�����ں���y=x-$\frac{1}{x}$��ֱ��AB����Ϊy=$\frac{3}{2}$��x-1�����Ӷ�|MN|=|=x-$\frac{1}{x}$-$\frac{3}{2}$��x-1��=$\frac{3}{2}$-��$\frac{x}{2}$+$\frac{1}{x}$����$\frac{3}{2}$-$\sqrt{2}$���ɴ�����������
��� �⣺���ں���y=sin$\frac{��}{3}$x��A��1��$\frac{\sqrt{3}}{2}$����B��2��$\frac{\sqrt{3}}{2}$����AB����Ϊy=$\frac{\sqrt{3}}{2}$��
�����Ǻ���ͼ�������ʿ�֪|MN|��1-$\frac{\sqrt{3}}{2}$��
���Խ��Ʒ�ֵΪ1-$\frac{\sqrt{3}}{2}$��
���ں���y=x-$\frac{1}{x}$����A��1��0����B��2��$\frac{3}{2}$����
��ֱ��AB����Ϊy=$\frac{3}{2}$��x-1����
��|MN|=|=x-$\frac{1}{x}$-$\frac{3}{2}$��x-1��=$\frac{3}{2}$-��$\frac{x}{2}$+$\frac{1}{x}$����$\frac{3}{2}$-$\sqrt{2}$��
���Խ��Ʒ�ֵΪ$\frac{3}{2}$-$\sqrt{2}$��
��ѡ��A��
���� ���⿼��ĺ��������Խ��Ʒ�ֵ�Ľ������ǻ����⣬����ʱҪ�������⣬ע�⺯�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | ���� | �ͳ� | ����ʱ�� | �����ص� |
| 17��3��10�� | �½�-���� | �½� | ���� | 20��00 | ��³ľ�� |
| 17��3��12�� | �½�-���� | �½� | ���� | 20��00 | ��³ľ�� |
| 17��3��15�� | ����-�½� | ���� | �½� | 20��00 | ��Ϫ |
| 17��3��17�� | ����-�½� | ���� | �½� | 20��00 | ��Ϫ |
| 17��3��19�� | ����-�½� | ���� | �½� | 20��00 | ��Ϫ |
| 17��3��22�� | �½�-���� | �½� | ���� | 20��00 | ��³ľ�� |
| 17��3��24�� | �½�-���� | �½� | ���� | 20��00 | ��³ľ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 1 | C�� | 18 | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ַDZ�Ҫ���� | B�� | ��Ҫ�dz������ | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
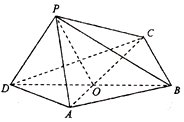 ��ͼ���ı���ABCD�У���BCDΪ�������Σ�AD=AB=2��BD=2$\sqrt{3}$��AC��BD����O�㣮����ACD�ر�AC����ʹD����P�㣬��֪PO��ƽ��ABCD���ɵĽ�Ϊ�ȣ���P����ƽ��ABCD�ڵ���Ӱ���ڡ�ACD�ڣ�
��ͼ���ı���ABCD�У���BCDΪ�������Σ�AD=AB=2��BD=2$\sqrt{3}$��AC��BD����O�㣮����ACD�ر�AC����ʹD����P�㣬��֪PO��ƽ��ABCD���ɵĽ�Ϊ�ȣ���P����ƽ��ABCD�ڵ���Ӱ���ڡ�ACD�ڣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com