
| A. | 4 | B. | 1 | C. | 18 | D. | $\frac{4}{5}$ |
分析 根据已知的约束条件画出满足约束条件的可行域,分析z=x2+y2表示的几何意义,结合图象即可给出z=x2+y2的最小值.
解答 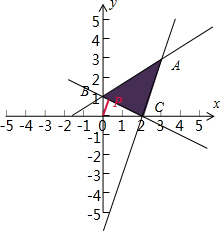 解:约束条件$\left\{\begin{array}{l}x+2y≥2\\ 3x-y-6≤0\\ 2x-3y+3≥0\end{array}\right.$,对应的平面区域如下图示:
解:约束条件$\left\{\begin{array}{l}x+2y≥2\\ 3x-y-6≤0\\ 2x-3y+3≥0\end{array}\right.$,对应的平面区域如下图示:
三角形顶点坐标分别为(3,3)、(0,1)和(2,0),
z=x2+y2表示可行域内的点(x,y)与原点(0,0)距离的平方,
由图可知|OP|2为z=x2+y2的最小值,此时z=x2+y2=$(\frac{2}{\sqrt{{1}^{2}+{2}^{2}}})^{2}$=$\frac{4}{5}$.
故选:D.
点评 平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.


科目:高中数学 来源: 题型:选择题
| A. | ω=2 | B. | 函数f(x)的对称轴为x=-$\frac{π}{2}$+kx(k∈Z) | ||
| C. | 函数f(x)的对称中心为($\frac{π}{2}$+kx,0)(k∈Z) | D. | 函数f(x)在[$\frac{π}{2}$,$\frac{2π}{3}$]上的最小值为-$\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
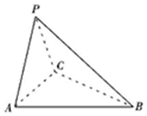 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$-$\sqrt{2}$ | B. | 1+$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$+$\sqrt{2}$ | C. | 1-$\sqrt{2}$,1+$\sqrt{2}$ | D. | 2-$\sqrt{2}$,2+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com