Question

（06年上海卷理）（16分）

已知有穷数列共有2项（整数≥2），首项＝2．设该数列的前项和为，且＝＋2（＝1，2，┅，2－1），其中常数＞1．

（1）求证：数列是等比数列；

（2）若＝2，数列满足＝（＝1，2，┅，2），求数列的通项公式；

（3）若（2）中的数列满足不等式|－|＋|－|＋┅＋|－|＋|－|≤4，求的值．

Answer 1

解析：(1)  [证明]   当n=1时,a₂=2a,则=a；

                  2≤n≤2k－1时, a_n+1=(a－1) S_n+2, a_n=(a－1) S_n－1+2,

                 a_n+1－a_n=(a－1) a_n,  ∴=a, ∴数列{a_n}是等比数列.

    (2) 解：由(1) 得a_n=2a, ∴a₁a₂…a_n=2a=2a=2,

             b_n=(n=1,2,…,2k).

   （3）设b_n≤,解得n≤k+,又n是正整数,于是当n≤k时, b_n<；

      当n≥k+1时, b_n>.

      原式=(－b₁)+(－b₂)+…+(－b_k)+(b_k+1－)+…+(b_2k－)

          =(b_k+1+…+b_2k)－(b₁+…+b_k)

          ==.

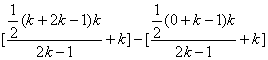         当≤4,得k²－8k+4≤0,    4－2≤k≤4+2,又k≥2,

∴当k=2,3,4,5,6,7时,原不等式成立.