B
分析:①联系偶函数和增函数得到函数在[0,1]上为减函数,从而可以判断;
②因为A、B是三角形的内角,所以A,B∈(0,π),在(0,π)上,y=cosx是减函数.由此知△ABC中,“A>B”?“cosA<cosB”,即可得答案;
③欲求f
-1(3),根据原函数的反函数为f
-1(x)知,只要求满足于f(x)=3的x的值即可;
④根据余弦定理表示出cosA,把已知得等式变形后代入即可求出cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数.
解答:①由已知可得函数在[0,1]上为减函数,∵
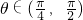
,∴1>sinθ>cosθ>0,∴f(sinθ)<f(cosθ),
故①错;
②∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),
∵在(0,π)上,y=cosx是减函数,∴△ABC中,“A>B”?“cosA<cosB”,故②正确;
③令f(t)=3,则t=f
-1(3)(-2≤t<0),所以有t
2+2=3,所以t=±1,因为-2≤t<0,所以t=-1,故③错误;
④∵b
2+c
2=a
2+bc,∴a
2=b
2+c
2-bc,
结合余弦定理知cosA=

=

=

,
又A∈(0,π),∴A=

,故④正确.
从而真命题有两个
故选B.
点评:本题的考点是命题的真假判断与应用,解题时需依据函数的性质,余弦定理一一判断,综合性强.

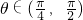 ,则f(sinθ)>f(cosθ);
,则f(sinθ)>f(cosθ); .
.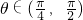 ,∴1>sinθ>cosθ>0,∴f(sinθ)<f(cosθ),
,∴1>sinθ>cosθ>0,∴f(sinθ)<f(cosθ), =
= =
= ,
, ,故④正确.
,故④正确.

 阅读快车系列答案
阅读快车系列答案 的单调递增区间是
的单调递增区间是 ;
; ,且cosα<sinβ,则
,且cosα<sinβ,则 ;
; ,则siny-cos2x的最大值是
,则siny-cos2x的最大值是 .
.