
分析 求出倾斜角是$\frac{π}{6}$的直线的斜率,设出直线方程,利用原点与直线的距离为$\frac{{\sqrt{3}}}{2}$,求出直线方程中的未知数,即可确定直线方程.
解答 解:因直线斜率为tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$,可设直线方程y=$\frac{\sqrt{3}}{3}$x+b,化为一般式$\frac{\sqrt{3}}{3}$x-y+b=0,
由原点到该直线的距离为$\frac{{\sqrt{3}}}{2}$,得$\frac{|b|}{\sqrt{\frac{1}{3}+1}}$=$\frac{\sqrt{3}}{2}$,解得b=±1,
∵直线l不经过第四象限,
∴b=1,
所以直线方程为$y=\frac{{\sqrt{3}}}{3}x+1$.
故答案为:$y=\frac{{\sqrt{3}}}{3}x+1$.
点评 本题考查点到直线的距离公式,考查计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
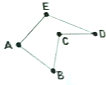 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{kn}{m}$ | B. | $\frac{km}{n}$ | C. | k+m-n | D. | k+m+n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
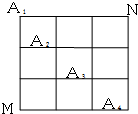 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}-\frac{1}{2}$i | B. | $\frac{3}{2}+\frac{1}{2}$i | C. | 3-i | D. | 3+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (-2,-1) | C. | (3,-1) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com