
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
分析 首先由已知的等式求出tanφ,然后计算定积分即可.
解答 解:由已知$\frac{1}{sinφ}$+$\frac{1}{cosφ}$=2$\sqrt{2}$,φ∈(0,$\frac{π}{2}$),
得到sinφ=cosφ=$\frac{\sqrt{2}}{2}$,所以tanφ=1,
所以${∫}_{-1}^{tanφ}$(x2-2x)dx=${∫}_{-1}^{1}$(x2-2x)dx=($\frac{1}{3}{x}^{3}-{x}^{2}$)|${\;}_{-1}^{1}$=$\frac{2}{3}$;
故选C.
点评 本题考查了三角函数值的求法以及定积分的计算;正确求出φ是解答的前提.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a∈R,f(x)为奇函数 | B. | ?a∈R,f(x)为奇函数 | ||
| C. | ?a∈R,f(x)不为偶函数 | D. | ?a∈R,f(x)不为偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,$BA\user1{∥}$平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,$PA=PD=\frac{{\sqrt{2}}}{2}CD=\sqrt{2}$.
如图,在四棱锥P-ABCD中,$BA\user1{∥}$平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,$PA=PD=\frac{{\sqrt{2}}}{2}CD=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
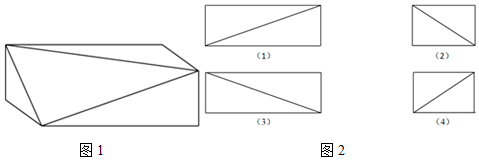
| A. | (1)(3)(4) | B. | (2)(4)(3) | C. | (1)(3)(2) | D. | (2)(4)(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com