
分析 化简函数f(x),根据函数图象的平移,得出函数解析式,利用图象关于y轴对称,求出ω的值与最小值.
解答 解:函数f(x)=sinωx+$\sqrt{3}$cosωx=2sin(ωx+$\frac{π}{3}$),
其图象向右平移$\frac{π}{6}$个单位后,得到
y=2sin[ω(x-$\frac{π}{6}$)+$\frac{π}{3}$]=2sin(ωx-$\frac{π}{6}$ω+$\frac{π}{3}$)的图象,
且该图象关于y轴对称,
所以-$\frac{π}{6}$ω+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,
解得ω=-6k-1,k∈Z;
又ω>0,
所以当k=-1时ω取得最小正整数5.
故答案为:5.
点评 本题考查了三角函数的化简与图象平移的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a∈[0,4] | B. | a∈(0,4) | C. | a∈(-4,0] | D. | a∈(-4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
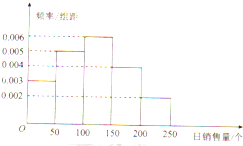 如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )
如图所示,一报刊亭根据某报纸以往的销售记录,绘制了日销售量的频率分布直方图,但原始数据遗失,则对日销售量中位数的估计值较为合理的是( )| A. | 100 | B. | 113 | C. | 117 | D. | 125 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com