
分析 (Ⅰ)由题意可知:c=2,又b=1,则a2=b2+c2=5,求得a,即可椭圆C的离心率;
(Ⅱ)当a=3,求得椭圆方程,丨PA丨2=(x-2)2+y2═$\frac{8}{9}$(x-$\frac{9}{4}$)2+$\frac{1}{2}$,(-3≤x≤3),根据二次函数图象及性质,即可求得|PA|的最大值与最小值.
解答 解:(Ⅰ)由条件可知c=2,又b=1,
∴a2=b2+c2=4+1=5,即a=$\sqrt{5}$,
∴离心率为e=$\frac{c}{a}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;…(4分)
(Ⅱ)若a=3,则椭圆方程为$\frac{{x}^{2}}{9}+{y}^{2}=1$,设P(x,y),
则丨PA丨2=(x-2)2+y2=(x-2)2+1-$\frac{{x}^{2}}{9}$=$\frac{8}{9}$(x-$\frac{9}{4}$)2+$\frac{1}{2}$,(-3≤x≤3)…(8分)
故当x=$\frac{9}{4}$时,丨PA丨min=$\frac{\sqrt{2}}{2}$;
当x=-3时,丨PA丨max=5.…(12分)(若未说明x的取值扣1分)
点评 本题考查椭圆的标准方程及简单几何性质,考查二次函数性质及最值,考查计算能力,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
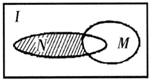 设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | (-∞,1) | C. | (1,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com