
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立的极坐标系中,曲线
轴正半轴为极轴建立的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 分别相交于异于原点的点
分别相交于异于原点的点![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,点![]() 为正方形
为正方形![]() 的中心,
的中心,![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
,![]() 是线段
是线段![]() 的中点,则( )
的中点,则( )

A.直线![]() ,
,![]() 是相交直线
是相交直线
B.直线![]() 与直线
与直线![]() 所成角等于
所成角等于![]()
C.直线![]() 与直线
与直线![]() 所成角等于直线
所成角等于直线![]() 与直线
与直线![]() 所成角
所成角
D.直线![]() 与平面
与平面![]() 所成角小于直线
所成角小于直线![]() 平面
平面![]() 所成角
所成角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线交抛物线
且斜率为1的直线交抛物线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)抛物线![]() 上一点
上一点![]() ,直线
,直线![]() (其中
(其中![]() )与抛物线
)与抛物线![]() 交于
交于![]() ,
,![]() 两个不同的点(
两个不同的点(![]() ,
,![]() 均不与点
均不与点![]() 重合).设直线
重合).设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() .直线
.直线![]() 是否过定点?如果是,请求出所有定点;如果不是,请说明理由.
是否过定点?如果是,请求出所有定点;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 斜率为
斜率为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,
点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,![]() ,
,![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BDE;
平面BDE;
![]() Ⅱ
Ⅱ![]() 求直线MN到平面BDE的距离;
求直线MN到平面BDE的距离;
![]() Ⅲ
Ⅲ![]() 求二面角
求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆C:
是椭圆C:![]() 上的一点,椭圆C的离心率与双曲线
上的一点,椭圆C的离心率与双曲线![]() 的离心率互为倒数,斜率为
的离心率互为倒数,斜率为![]() 直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
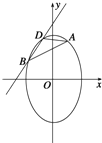
(1)求椭圆C的方程;
(2)若![]() 分别为直线AB,AD的斜率,求证:
分别为直线AB,AD的斜率,求证:![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对职工开展了安全知识竞赛的活动,将竞赛成绩按照![]() ,
,![]() ,… ,
,… ,![]() 分成
分成![]() 组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )
组,得到下面频率分布直方图.根据频率分布直方图.下列说法正确的是( )

①根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的众数估计值为![]() ;
;
②根据频率分布直方图估计该商场的职工的安全知识竞赛的成绩的中位数约为![]() ;
;
③若该商场有![]() 名职工,考试成绩在
名职工,考试成绩在![]() 分以下的被解雇,则解雇的职工有
分以下的被解雇,则解雇的职工有![]() 人;
人;
④若该商场有![]() 名职工,商场规定只有安全知识竞赛超过
名职工,商场规定只有安全知识竞赛超过![]() 分(包括
分(包括![]() 分)的人员才能成为安全科成员,则安全科成员有
分)的人员才能成为安全科成员,则安全科成员有![]() 人.
人.
A.①③B.②③C.②④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com