解:(1)f(x)=x
3-(a+b)x
2+abx,∴f'(x)=3x
2-2(a+b)x+ab=0的两根为s,t,
令f'(x)=g(x),∵0<a<b,∴g(0)=ab>0,g(a)=a(a-b)<0,g(b)=b(b-a)>0,
故有0<s<a<t<b.
(2)设AB中点C(x
0,y
0),则
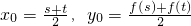
,
故有
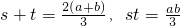
,∴
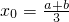
,
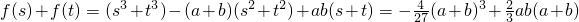
.
∴
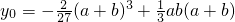
.
代入验算可知C在曲线y=f(x)上.
(3)过曲线上的点(x
1,y
1)的切线的斜率是3
1x
2-2(a+b)x
1+ab,
当x
1=0时,切线的斜率k
1=ab;
当x
1≠0时,
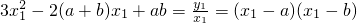
,∴
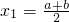
,
∴切线斜率
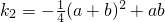
.
∵
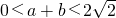
,∴
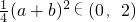
,∴k
2>(ab-2)
∴k
1k
2=abk
2>ab(ab-2)=(ab-1)
2-1≥-1
∴k
1k
2≠-1,故过原点且与曲线相切的两条直线不可能垂直.
分析:(1)根据函数的极值点出导数为0,知,极值点是导数等于零的根,所以先求导,再解导数等于零,两根为s,t,再判断x=a,b时导数的正负,比较大小即可.
(2)求出AB的中点坐标,再代入y=f(x),判断是否成立即可.
(3)如果两条切线互相垂直,则斜率乘积等于-1,所以要证两条切线不可能垂直,只需证明它们斜率之积不等于-1即可,利用曲线的切线斜率是该点处的导数来计算.
点评:本题主要考查导数,切线极值 知识,属于基础知识,基本运算的考查.

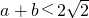 ,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.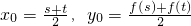 ,
,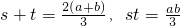 ,∴
,∴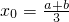 ,
,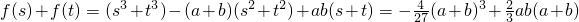 .
.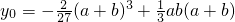 .
.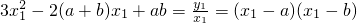 ,∴
,∴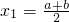 ,
,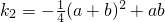 .
.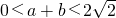 ,∴
,∴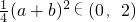 ,∴k2>(ab-2)
,∴k2>(ab-2)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<