
分析 (Ⅰ)设h(x)=lnx-$\frac{1}{2}$x2-(a-$\frac{1}{a}$)x,求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出函数的最大值=-lna+$\frac{1}{{2a}^{2}}$-1=0;从而求出代数式的值;
(Ⅱ)求出切线l的方程,得到a═$\frac{1}{{x}_{1}}$-$\frac{1}{e}$,且lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0,令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$,根据函数的单调性证明即可;
(Ⅲ)先求出g(x)的导数,通过讨论a的范围,结合函数的单调性从而得到答案.
解答 解:(Ⅰ)∵f(x)=$\frac{1}{2}$x2-$\frac{1}{a}$x+a,
∴lnx-$\frac{1}{2}$x2-(a-$\frac{1}{a}$)x=0,
设h(x)=lnx-$\frac{1}{2}$x2-(a-$\frac{1}{a}$)x,则h′(x)=-$\frac{(x+a)(x-\frac{1}{a})}{x}$,
a>0时,h(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,+∞)递减,
则h(x)max=h($\frac{1}{a}$)=-lna+$\frac{1}{{2a}^{2}}$-1,
∵h(x)=0有唯一实根,
∴x0=$\frac{1}{a}$且h(x)max=h($\frac{1}{a}$)=-lna+$\frac{1}{{2a}^{2}}$-1=0;
故1+lna=$\frac{1}{{2a}^{2}}$,∴(1+lna)a2=$\frac{1}{2}$;
(Ⅱ)证明:∵过原点所作曲线y=f(x)的切线l与直线y=-ex+1垂直,
∴切线l的斜率为k=$\frac{1}{e}$,方程是y=$\frac{1}{e}$x,
设l与y=f(x)的切点为(x1,y1),
∴$\left\{\begin{array}{l}{f′{(x}_{1})=\frac{1}{e}}\\{{y}_{1}=l{nx}_{1}-a{(x}_{1}-1)}\\{{y}_{1}={\frac{1}{e}x}_{1}}\end{array}\right.$,
∴a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$,且lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0,
令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$,则m′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$,
∴m(x)在(0,1)递减,在(1,+∞)递增,
若x1∈(0,1),∵m($\frac{1}{e}$)=-2+e-$\frac{1}{e}$>0,m(1)=-$\frac{1}{e}$<0,
∴x1∈($\frac{1}{e}$,1),
而a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$在x1∈($\frac{1}{e}$,1)递减,
∴$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$,
若x1∈(1,+∞),∵m(x)在(1,+∞)递增,且m(e)=0,则x1=e,
∴a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0(舍),
综上:$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$;
(Ⅲ)∵g(x)=f(x+1)+ex=ln(x+1)-ax+ex,
∴g′(x)=$\frac{1}{x+1}$-a+ex,g″(x)=$\frac{{{e}^{x}(x+1)}^{2}-1}{{(x+1)}^{2}}$≥0,
①0<a≤2时,∵g′(x)在[0,+∞)递增,
∴g′(x)≥g′(0)=2-a≥0,
∴g(x)在[0,+∞)递增,g(x)≥g(0)=1恒成立,符合题意,
②a>2时,∵g′(x)在[0,+∞)递增,g′(0)=2-a<0,
则存在x0(0,+∞),使得g′(x0)=0,
∴g(x)在(0,x0)递减,在(x0,+∞)递增,
又x∈(0,x0)时,g(x)<g(0)=1,
∴g(x)≥1不恒成立,不合题意,
综上,所求实数a的范围是(0,2].
点评 本题考查了函数的单调性、极值问题,考查了导数的应用,考查曲线的切线方程问题,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 过圆O外一点P,作圆的切线PA、PB,A、B为切点,M为弦AB上一点,过M作直线分别交PA、PB于点C、D.
过圆O外一点P,作圆的切线PA、PB,A、B为切点,M为弦AB上一点,过M作直线分别交PA、PB于点C、D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
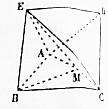 如图,在四梭锥A-BCDE中,EB=EA=AB=BC.,∠EBC=90°,M为AC的中点,AB⊥EM.
如图,在四梭锥A-BCDE中,EB=EA=AB=BC.,∠EBC=90°,M为AC的中点,AB⊥EM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com