
分析 (Ⅰ)求出导函数,对导函数二次求导,得出导函数的最小值为$\frac{1}{2}$>0,判断原函数递增;
(Ⅱ)二次求导,得出导函数递增,对1-a进行分类讨论,得出a的范围;
(Ⅲ)求出F(x)=ex+e-x,利用放缩法判断$F({x_1})F({x_2})={e^{{x_1}+{x_2}}}+{e^{-({x_1}+{x_2})}}+{e^{{x_1}-{x_2}}}+{e^{-{x_1}+{x_2}}}>{e^{{x_1}+{x_2}}}+{e^{-({x_1}+{x_2})}}+2>{e^{{x_1}+{x_2}}}+2$
得出F(1)F(n)>en+1+2,…F(n)F(1)>en+1+2.最后得出结论.
解答 (Ⅰ)解:$f'(x)={e^x}-x-\frac{1}{2}$,令g(x)=f'(x),则g'(x)=ex-1,
则当x∈(-∞,0)时,g'(x)<0,f'(x)单调递减,
当x∈(0,+∞)时,g'(x)>0,f'(x)单调递增.
所以有$f'(x)≥f'(0)=\frac{1}{2}>0$,所以f(x)在(-∞,+∞)上递增…(4分)
(Ⅱ)解:当x≥0时,f'(x)=ex-x-a,令g(x)=f'(x),
则g'(x)=ex-1≥0,则f'(x)单调递增,f'(x)≥f'(0)=1-a
当a≤1即f'(x)≥f'(0)=1-a≥0时,f(x)在(0,+∞)上递增,f(x)≥f(0)=0成立;
当a>1时,存在x0∈(0,+∞),使f'(x0)=0,
则f(x)在(0,x0)上递减,则当x∈(0,x0)时,f(x)<f(0)<0,不合题意.
综上a≤1.(8分)
(Ⅲ)证明:∵F(x)=ex+e-x,
∴$F({x_1})F({x_2})={e^{{x_1}+{x_2}}}+{e^{-({x_1}+{x_2})}}+{e^{{x_1}-{x_2}}}+{e^{-{x_1}+{x_2}}}>{e^{{x_1}+{x_2}}}+{e^{-({x_1}+{x_2})}}+2>{e^{{x_1}+{x_2}}}+2$
∴F(1)F(n)>en+1+2,F(2)F(n-1)>en+1+2
…F(n)F(1)>en+1+2.
由此得,[F(1)F(2)…F(n)]2=[F(1)F(n)]•[F(2)F(n-1)]•…•[F(n)F(1)]>(en+1+2)n
故$F(1)•F(2)•…•F(n)>{({e^{n+1}}+2)^{\frac{n}{2}}}$(n∈N*).
点评 本题考查了导函数的二次求导,导函数的分类讨论问题和放缩法的应用,难点是对函数的构造和放缩的应用.


科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC=BC,四边形ABB1A1是边长为1的正方形,若E,F分别是CB1,BA1的中点.
如图,直三棱柱ABC-A1B1C1中,AC=BC,四边形ABB1A1是边长为1的正方形,若E,F分别是CB1,BA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
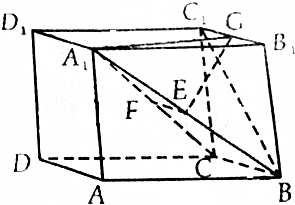 如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.
如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com