
分析 曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}\right.$(α为参数),消去参数化为普通方程.曲线C2的极坐标方程为ρsin(θ+$\frac{π}{4}$)=4$\sqrt{2}$,展开化为:$\frac{\sqrt{2}}{2}ρ$(sinθ+cosθ)=4$\sqrt{2}$,利用互化公式化为普通方程x+y-8=0.设与直线x+y-8=0平行且与椭圆相切的直线方程为:x+y+m=0.与椭圆方程联立,利用相切的性质解得m,即可得出.
解答 解:曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}\right.$(α为参数),消去参数化为:$\frac{{x}^{2}}{3}+{y}^{2}$=1.
曲线C2的极坐标方程为ρsin(θ+$\frac{π}{4}$)=4$\sqrt{2}$,展开化为:$\frac{\sqrt{2}}{2}ρ$(sinθ+cosθ)=4$\sqrt{2}$,化为x+y-8=0.
设与直线x+y-8=0平行且与椭圆相切的直线方程为:x+y+m=0.
联立$\left\{\begin{array}{l}{x+y+m=0}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$,化为:4x2+6mx+3m2-3=0,(*)
由△=36m2-16(3m2-3)=0,解得m=±2,
取m=-2,代入(*)可得:(2x-3)2=0,解得x=$\frac{3}{2}$,代入x+y-2=0,解得y=$\frac{1}{2}$.
∴切点P$(\frac{3}{2},\frac{1}{2})$满足条件.
故答案为:$(\frac{3}{2},\frac{1}{2})$.
点评 本题考查了参数方程与普通方程的互化、极坐标化为直角坐标方程、直线与椭圆相切的性质、平行线之间的距离,考查了推理能力与计算能力,属于中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
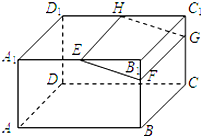 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )| A. | $\frac{11}{12}$ | B. | $\frac{3}{4}$ | C. | $\frac{13}{16}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用智能手机 | 不使用智能手机 | 合计 | |
| 学习成绩优秀 | 4 | 8 | 12 |
| 学习成绩不优秀 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为使用智能手机对学习有影响 | |
| B. | 有99.5%的把握认为使用智能手机对学习无影响 | |
| C. | 有99.9%的把握认为使用智能手机对学习有影响 | |
| D. | 有99.9%的把握认为使用智能手机对学习无影响 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com