
分析 (Ⅰ)根据绝对值的几何运用,分类讨论,求得f(x)≤x的解集.
(Ⅱ)x∈[-2,-1]时,f(x)=x+3,最小值为1,再根据t2-t≤1,求得实数t的取值范围.
解答 解:(Ⅰ)x≤-$\frac{1}{2}$时,x+3≤x,不成立;
-$\frac{1}{2}$<x<2时,-3x+1≤x,解得x≥$\frac{1}{4}$,∴$\frac{1}{4}$≤x<2;
x≥2时,-x-3≤x,∴x≥-$\frac{3}{2}$,∴x≥2,
综上所述,不等式f(x)≤x的解集为[$\frac{1}{4}$,+∞);
(II )x∈[-2,-1]时,f(x)=x+3,最小值为1.
∵不等式f(x)≥t2-t在x∈[-2,-1]时恒成立,
∴t2-t≤1,
∴$\frac{1-\sqrt{5}}{2}$≤t≤$\frac{1+\sqrt{5}}{2}$.
点评 本题考查绝对值不等式的解法,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | x1•x3=x22 | B. | x1•x3<x22 | C. | x1•x3>x22 | D. | x1•x3≥x22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\frac{{2\sqrt{2}}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{3\sqrt{2}}}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
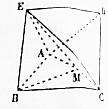 如图,在四梭锥A-BCDE中,EB=EA=AB=BC.,∠EBC=90°,M为AC的中点,AB⊥EM.
如图,在四梭锥A-BCDE中,EB=EA=AB=BC.,∠EBC=90°,M为AC的中点,AB⊥EM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
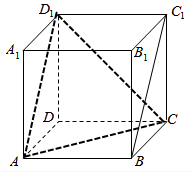 如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,平面AD1C把正方体分成两部分.求:
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,平面AD1C把正方体分成两部分.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
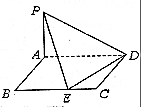 如图,矩形ABCD所在平面与平面PAD垂直,PA⊥AD,且AD=2AB,E为BC上的动点.
如图,矩形ABCD所在平面与平面PAD垂直,PA⊥AD,且AD=2AB,E为BC上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com