
 过圆O外一点P,作圆的切线PA、PB,A、B为切点,M为弦AB上一点,过M作直线分别交PA、PB于点C、D.
过圆O外一点P,作圆的切线PA、PB,A、B为切点,M为弦AB上一点,过M作直线分别交PA、PB于点C、D.分析 (Ⅰ)过点C作CE∥PD交AB于点E,运用两直线平行的性质定理和相似三角形的判定和性质,结合圆的切线的性质:切线长相等,即可求得MD;
(Ⅱ)连接OA、OB、OC、OD,运用切线的性质,证得四点A、C、M、O共圆,四点B、D、O、M共圆,可得同弧所对的圆周角相等,再由等腰三角形的三线合一,即可得证.
解答  解:(Ⅰ)如图1,
解:(Ⅰ)如图1,
过点C作CE∥PD交AB于点E,
则∠PBA=∠CEA,
且△MCE∽△MDB,
所以$\frac{MC}{MD}=\frac{EC}{BD}$.
因为PA、PB是圆的切线,
所以∠PAB=∠PBA,
所以∠PAB=∠CEA,
从而$AC=EC,\frac{MC}{MD}=\frac{AC}{BD}$,
得$MD=\frac{MC}{AC}•BD$=$\frac{4×2}{3}$=$\frac{8}{3}$;
证明:(Ⅱ)如图2,连接OA、OB、OC、OD,
则OA⊥PA,OB⊥PB.
因为MO⊥CD,所以∠OMD=∠OBD=∠OMC=∠OAC=90°,
故四点A、C、M、O共圆,四点B、D、O、M共圆,
所以∠OCM=∠OAM,∠ODM=∠OBM.
又OA=OB,
所以∠OAM=∠OBM,
故∠OCM=∠ODM,OC=OD.
从而MD=MC.
点评 本题考查相似三角形的判定和性质定理的运用,考查四点共圆的判定和圆的切线的性质及同弧所对圆周角相等,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
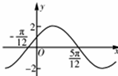 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):| A. | ①③ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∪(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC=BC,四边形ABB1A1是边长为1的正方形,若E,F分别是CB1,BA1的中点.
如图,直三棱柱ABC-A1B1C1中,AC=BC,四边形ABB1A1是边长为1的正方形,若E,F分别是CB1,BA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com