
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换.
(1)求矩阵M的特征值及相应的特征向量.
(2)求逆矩阵M-1以及椭圆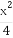 +
+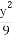 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
数列{an}的前n项和Sn=2n-1,则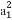 +
+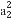 +
+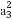 +…+
+…+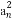 等于( )
等于( )
(A)(2n-1)2(B) (2n-1)2
(2n-1)2
(C)4n-1(D) (4n-1)
(4n-1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
在等差数列{an}中,已知a4+a8=16,则a2+a10=( )
(A)12(B)16(C)20(D)24
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
曲线x2-4y2=16在y轴方向上进行伸缩变换,伸缩系数k=2,求变换后的曲线方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷(解析版) 题型:解答题
已知y=f(x)的图象(如图1)经A=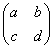 作用后变换为曲线C(如图2).
作用后变换为曲线C(如图2).
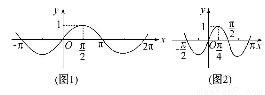
(1)求矩阵A. (2)求矩阵A的特征值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
已知椭圆C的极坐标方程为ρ2=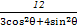 ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为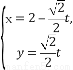 (t为参数,t∈R).
(t为参数,t∈R).
(1)求直线l和曲线C的普通方程.
(2)求点F1,F2到直线l的距离之和.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
已知两曲线参数方程分别为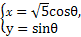 (0≤θ<π)和
(0≤θ<π)和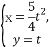 (t∈R),求它们的交点坐标.
(t∈R),求它们的交点坐标.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,a,b,c∈(0,1),且无其他得分情况,已知他投篮一次得分的数学期望为1,则ab的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
将下列各极坐标方程化为直角坐标方程.
(1)θ= (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com