
【题目】设等比数列{an}的前项n和Sn , a2= ![]() ,且S1+
,且S1+ ![]() ,S2 , S3成等差数列,数列{bn}满足bn=2n.
,S2 , S3成等差数列,数列{bn}满足bn=2n.
(1)求数列{an}的通项公式;
(2)设cn=anbn , 若对任意n∈N+ , 不等式c1+c2+…+cn≥ ![]() λ+2Sn﹣1恒成立,求λ的取值范围.
λ+2Sn﹣1恒成立,求λ的取值范围.
【答案】
(1)解:设数列{an}的公比为q,
∵ ![]() 成等差数列,∴
成等差数列,∴ ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]()
(2)解:设数列{cn}的前项n和为Tn,则Tn=c1+c2+c3+…+cn,
又 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
两式相减得 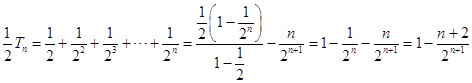 ,
,
∴ ![]() ,
,
又 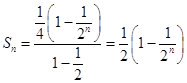 ,
,
∴对任意n∈N+,不等式 ![]() 恒成立等价于
恒成立等价于 ![]() 恒成立,
恒成立,
即 ![]() 恒成立,即
恒成立,即 ![]() 恒成立,
恒成立,
令 ![]() ,
, ![]() ,
,
∴f(n)关于n单调递减,∴ ![]() ,∴λ≤2,
,∴λ≤2,
∴λ的取值范围为(﹣∞,2]
【解析】(1)由S1+ ![]() ,S2 , S3成等差数列,可得
,S2 , S3成等差数列,可得 ![]() ,化简为
,化简为 ![]() ,又因为
,又因为 ![]() ,解得a1和q,即可求出等比数列{an}的通项公式;(2)因为{an}是等比数列,{bn}是等差数列,而cn=anbn , 故利用错位相减法即可求出Tn=c1+c2+…+cn , 将Tn和Sn代入不等式,并整理得
,解得a1和q,即可求出等比数列{an}的通项公式;(2)因为{an}是等比数列,{bn}是等差数列,而cn=anbn , 故利用错位相减法即可求出Tn=c1+c2+…+cn , 将Tn和Sn代入不等式,并整理得 ![]() ,记f(n)=
,记f(n)= ![]() ,
,
利用作差法可得f(n)关于n单调递减,则f(n)max=f(1)=1,故 ![]() ,即λ≤2.
,即λ≤2.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣ax﹣2>0的解集为{x|x<﹣1或x>b}(b>﹣1).
(1)求a,b的值;
(2)当m>﹣ ![]() 时,解关于x的不等式(mx+a)(x﹣b)>0.
时,解关于x的不等式(mx+a)(x﹣b)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(﹣5,a)作圆x2+y2﹣2ax+2y﹣1=0的两条切线,切点分别为M(x1 , y1),N(x2 , y2),且 ![]() +
+ ![]() =0,则实数a的值为 .
=0,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(﹣1,1)上的增函数f(x)= ![]() 为奇函数,且f(
为奇函数,且f( ![]() )=
)= ![]()
(1)求函数f(x)的解析式;
(2)解关于t的不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( ) 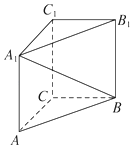
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com