
分析 根据题意,先将3人全排列,排好后有2个空位,将4张空椅子分成2组,插入空位,再将剩余的两把椅子插入,分“分别插入两个空位”与“插入同一个空位”两种情况分析,进而由分步计数原理,可得答案.
解答 解:根据题意,用×表示人,用□表示空椅子,
先将3人全排列,排好后有2个空位,将4张空椅子分成2组,插入空位,
排列如图(×□□×□□×),这时共占据了7张椅子,
还有2张空椅子,分2种情况讨论:
①将剩余的2张椅子分别插入两个空位,
如图中箭头所示(↓×□↓□×□↓□×↓),
即从4个空当中选2个插入,有C42种插法;
②2张插入同一个空位,有C41种插法,
再考虑3人可交换有A33种方法,
所以,共有A33(C42+C41)=60(种).
故答案为:60.
点评 本题考查排列、组合的应用,注意要先满足“相邻2人之间至少有2个空座位”的条件.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
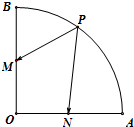 如图,扇形AOB中,OA=1,∠AOB=90°M是OB中点,P是弧$\widehat{AB}$上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值是1-$\frac{\sqrt{5}}{2}$.
如图,扇形AOB中,OA=1,∠AOB=90°M是OB中点,P是弧$\widehat{AB}$上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值是1-$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 图中程序是计算2+3+4+5+6的值的程序.在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是( )
图中程序是计算2+3+4+5+6的值的程序.在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是( )| A. | ①i>1 ②i=i-1 | B. | ①i>1 ②i=i+1 | C. | ①i>=1 ②i=i+1 | D. | ①i>=1 ②i=i-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x2)′=x | B. | (${\frac{1}{x}}$)′=-$\frac{1}{x^2}$ | C. | (${\sqrt{x}}$)′=$\frac{1}{{\sqrt{x}}}$ | D. | (ln2)′=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com