
分析 将函数进行化简,结合三角函数的图象和性质,以及函数是偶函数的特征即可得到答案.
解答 解:∵f(x)=sin(x+θ)+√3cos(x-θ)
f(x)=sinxcosθ+cosxsinθ+√3cosxcosθ+√3sinxsinθ
f(-x)=-sinxcosθ+cosxsinθ+√3cosxcosθ-√3sinxsinθ
∵f(x)是偶函数,f(x)=f(-x)
∴cosθ+√3sinθ=0
化简得:2sin(θ+$\frac{π}{6}$)=0
∴θ+$\frac{π}{6}$=0+kπ,(k∈Z)
解得∴θ=kπ-$\frac{π}{6}$,(k∈Z)
故答案为θ=kπ-$\frac{π}{6}$,(k∈Z)
点评 本题考查三角函数的两角和与差的公式进行化简,以及利用函数是偶函数的特征进行解题.属于基础题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
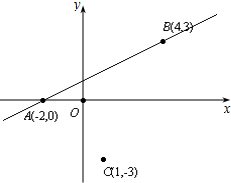 直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).
直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“幂函数f(x)=(m2-m-1)xm在(0,+∞)上为增函数,则m=-1”为真命题 | |
| C. | 命题“若x=y则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com