
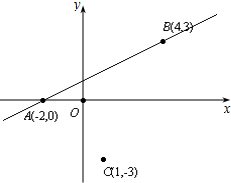
 直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).
直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).分析 (1)根据平面向量的坐标表示与数量积运算,列出方程即可求出t的值;
(2)【解法一】根据题意求出AC与AB的斜率,写出斜率k的取值范围,即可求出倾斜角θ的取值范围;
【解发二】讨论t的取值,求出直线CM的斜率取值范围,即可求出倾斜角的取值范围.
解答 解:(1)根据平面向量的坐标表示得,
$\overrightarrow{AB}$=(6,3),$\overrightarrow{AM}$=t$\overrightarrow{AB}$=(6t,3t),
$\overrightarrow{AC}$=(3,-3),$\overrightarrow{CM}$=$\overrightarrow{AM}$-$\overrightarrow{AC}$=(6t-3,3t+3),
∵$\overrightarrow{CM}$⊥$\overrightarrow{AB}$,∴$\overrightarrow{CM}$•$\overrightarrow{AB}$=45t-9=0,
∴t=$\frac{1}{5}$;(4分)
(2)【解法一】点M在线段AB上,AC的斜率k1=-1,AB的斜率k2=2,
∴直线CM的斜率满足k≤-1,或k≥2,(8分)
∴倾斜角θ∈[arctan2,$\frac{3π}{4}$];(10分)
【解法二】当t=$\frac{1}{2}$时,CM的斜率不存在;
当t≠$\frac{1}{2}$时,CM的斜率k=$\frac{t+1}{2t-1}$=$\frac{1}{2}$+$\frac{\frac{3}{2}}{2t-1}$在区间$[0,\frac{1}{2})$和$(\frac{1}{2},1]$单调递减,(7分)
∴k∈(-∞,-1]∪[2,+∞],
倾斜角θ∈[arctan2,$\frac{3π}{4}$].(10分)
点评 本题考查了平面向量的坐标表示与数量积的应用问题,也考查了直线的斜率与倾斜角的应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
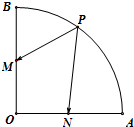 如图,扇形AOB中,OA=1,∠AOB=90°M是OB中点,P是弧$\widehat{AB}$上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值是1-$\frac{\sqrt{5}}{2}$.
如图,扇形AOB中,OA=1,∠AOB=90°M是OB中点,P是弧$\widehat{AB}$上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最小值是1-$\frac{\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com