
分析 先求出函数f(x)的值域,然后求出[f(x)-$\frac{1}{2}$]的值,再求出f(-x)的值域,然后求出[f(-x)-$\frac{1}{2}$]的值,最后求出g(x)=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]的值域即可.
解答 解:f(x)=$\frac{{2}^{x}}{{2}^{x}+1}$=1-$\frac{1}{{2}^{x}+1}$∈(0,1),
∴f(x)-$\frac{1}{2}$∈(-$\frac{1}{2}$,$\frac{1}{2}$),
[f(x)-$\frac{1}{2}$]=0 或-1,
∵f(-x)=$\frac{1}{{2}^{x}+1}$∈(0,1),
∴f(-x)-$\frac{1}{2}$∈(-$\frac{1}{2}$,$\frac{1}{2}$),
则[f(-x)-$\frac{1}{2}$]=-1或0,
∴g(x)=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]的值域为{0,-1}.
故答案为:{0,-1}.
点评 本题主要考查了函数的值域,同时考查分类讨论的数学思想,分析问题解决问题的能力,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
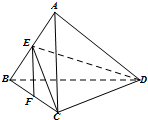 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{15}}{2π}$倍 | B. | $\frac{\sqrt{15}}{π}$倍 | C. | $\frac{\sqrt{2}}{π}$倍 | D. | $\frac{2\sqrt{2}}{π}$倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
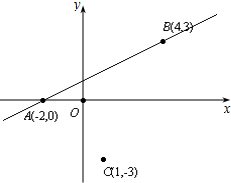 直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).
直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a不一定平行于b | |
| B. | 若α不垂直于β,则α内一定不存在直线垂直于β | |
| C. | 若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ | |
| D. | 若α⊥β,则α内一定不存在直线平行于β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com