
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的焦距为2,且经过点
的焦距为2,且经过点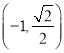 ,过左焦点
,过左焦点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,
,![]() 两点.
两点.
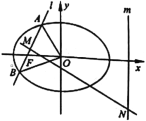
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() ,
,![]() ,
,![]() 的斜率之和为0,求直线
的斜率之和为0,求直线![]() 的方程;
的方程;
(3)设弦![]() 的垂直平分线分别与直线
的垂直平分线分别与直线![]() ,椭圆
,椭圆![]() 的右准线
的右准线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据已知求出![]() 的值,即得椭圆的
的值,即得椭圆的![]() 的方程;(2)设直线
的方程;(2)设直线![]() :
:![]() ,
,![]() ,联立直线和椭圆的方程得到韦达定理,根据直线
,联立直线和椭圆的方程得到韦达定理,根据直线![]() ,
,![]() ,
,![]() 的斜率之和为0,求出
的斜率之和为0,求出![]() ,即得直线的方程;(3)直线
,即得直线的方程;(3)直线![]() 的斜率不存在时,
的斜率不存在时,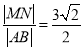 ;直线
;直线![]() 的斜率存在时,求出
的斜率存在时,求出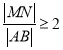 .即得解.
.即得解.
(1)因为椭圆![]() 的焦距为2,所以椭圆
的焦距为2,所以椭圆![]() 的焦点为
的焦点为![]() ,
,
所以点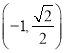 到焦点
到焦点![]() ,
,![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,
故![]() ,得
,得![]() .
.
所以![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)依题意,左焦点![]() ,设直线
,设直线![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() .
.
联立方程组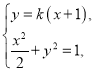 整理得
整理得![]() ,
,
所以![]() ,
,![]() .
.
因为直线![]() ,
,![]() ,
,![]() 的斜率之和为0,所以
的斜率之和为0,所以![]() ,
,
即![]() ,整理得
,整理得![]() ,
,
即![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
(3)若直线![]() 的斜率不存在,
的斜率不存在,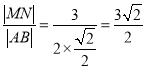 ;
;
若直线![]() 的斜率存在,由(2)可得
的斜率存在,由(2)可得![]()
![]()
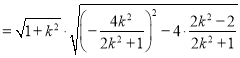
![]() ,
,
又![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
所以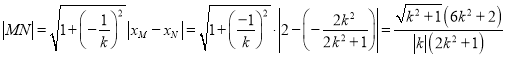 .
.
故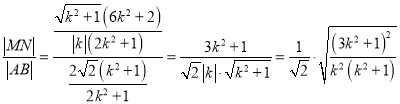 ,
,
令![]() ,则
,则![]() ,
,
故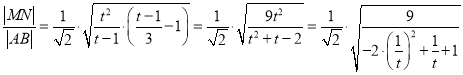
当![]() 时,
时,![]() ,
,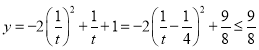 ,
,
所以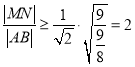 .
.
显然,![]() ,
,
所以![]() 的最小值为2.
的最小值为2.


科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
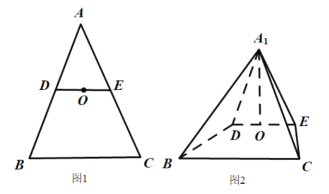
(1)求证:![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() =k在(0,+∞)上有两个不同的解α,β(α<β),则下列的四个命题正确的是( )
=k在(0,+∞)上有两个不同的解α,β(α<β),则下列的四个命题正确的是( )
A. sin 2α=2αcos2α B. cos 2α=2αsin2α
C. sin 2β=-2βsin2β D. cos 2β=-2βsin2β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率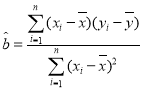 ;相关系数
;相关系数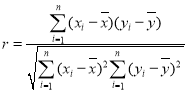 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 与
与![]() 的图象上存在关于原点对称的点,求实数
的图象上存在关于原点对称的点,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,已知
,已知![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com