已知函数f(x)=x-1ex的定义域是(0,+∞).
(1)求函数f(x)在[m,m+1](m>0)上的最小值;
(2)?x∈(0,+∞),不等式xf(x)>-x2+λx-1恒成立,求实数λ的取值范围.
解:(1)
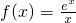
,∴
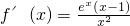
.
当x∈(0,1)时,∴f(x)在(0,1]上递减;
当x∈(1,+∞)时,∴f(x)在[1,+∞)上递增.
∴当m≥1时,f(x)在[m,m+1]上递增,

;
当0<m<1时,f(x)在[m,1]上递减,在[1,m+1]上递增,f(x)
min=f(1)=e.
∴
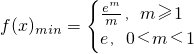
.
(2)?x>0,e
x>-x
2+λx-1恒成立,即
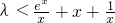
恒成立.
由(1)可知,
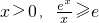
,当且仅当x=1时取等号,
又
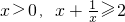
,当且仅当x=1时取等号,
∴当且仅当x=1时,有
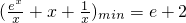
.
∴λ<e+2.
分析:(1)先求导函数,根据函数的定义域,可知当x∈(0,1)时,f(x)在(0,1]上递减;当x∈(1,+∞)时,f(x)在[1,+∞)上递增.从而可确定函数f(x)在[m,m+1](m>0)上的最小值;
(2)利用分离参数法,问题可转化为?x>0,
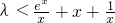
恒成立.由于
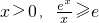
,当且仅当x=1时取等号,
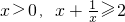
,当且仅当x=1时取等号,从而可知当x=1时,有
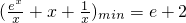
,故可求实数λ的取值范围.
点评:本题以函数为载体,考查利用导数求单调性,考查函数的最值,考查基本不等式的运用,考查恒成立问题的处理.

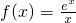 ,∴
,∴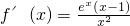 .
. ;
;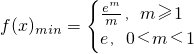 .
.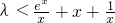 恒成立.
恒成立.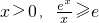 ,当且仅当x=1时取等号,
,当且仅当x=1时取等号,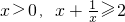 ,当且仅当x=1时取等号,
,当且仅当x=1时取等号,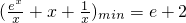 .
.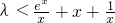 恒成立.由于
恒成立.由于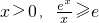 ,当且仅当x=1时取等号,
,当且仅当x=1时取等号,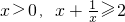 ,当且仅当x=1时取等号,从而可知当x=1时,有
,当且仅当x=1时取等号,从而可知当x=1时,有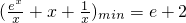 ,故可求实数λ的取值范围.
,故可求实数λ的取值范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<