
ЁОЬтФПЁПЭждВЙцЪЧЛЭждВЕФвЛжжЙЄОпЃЌШчЭМ1ЫљЪОЃЌдкЪЎзжаЮЛЌВлЩЯИїгавЛИіЛюЖЏЛЌБъ![]() ЃЌ
ЃЌ![]() ЃЌгавЛИља§ИЫНЋСНИіЛЌБъСЌГЩвЛЬхЃЌ
ЃЌгавЛИља§ИЫНЋСНИіЛЌБъСЌГЩвЛЬхЃЌ![]() ЃЌ
ЃЌ![]() ЮЊа§ИЫЩЯЕФвЛЕуЃЌЧвдк
ЮЊа§ИЫЩЯЕФвЛЕуЃЌЧвдк![]() ЃЌ
ЃЌ![]() СНЕужЎМфЃЌЧв
СНЕужЎМфЃЌЧв![]() ЃЌЕБЛЌБъ
ЃЌЕБЛЌБъ![]() дкЛЌВл
дкЛЌВл![]() ФкзїЭљИДдЫЖЏЃЌЛЌБъ
ФкзїЭљИДдЫЖЏЃЌЛЌБъ![]() дкЛЌВл
дкЛЌВл![]() ФкЫцжЎдЫЖЏЪБЃЌНЋБЪМтЗХжУгк
ФкЫцжЎдЫЖЏЪБЃЌНЋБЪМтЗХжУгк![]() ДІПЩЛГіЭждВЃЌМЧИУЭждВЮЊ
ДІПЩЛГіЭждВЃЌМЧИУЭждВЮЊ![]() .ШчЭМ2ЫљЪОЃЌЩш
.ШчЭМ2ЫљЪОЃЌЩш![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌвд
ЃЌвд![]() ЫљдкЕФжБЯпЮЊ
ЫљдкЕФжБЯпЮЊ![]() жсЃЌвд
жсЃЌвд![]() ЫљдкЕФжБЯпЮЊ
ЫљдкЕФжБЯпЮЊ![]() жсЃЌНЈСЂЦНУцжБНЧзјБъЯЕ.
жсЃЌНЈСЂЦНУцжБНЧзјБъЯЕ.

ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЪЧЭждВ
ЪЧЭждВ![]() ЕФзѓгвЖЅЕуЃЌЕу
ЕФзѓгвЖЅЕуЃЌЕу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯЕФЖЏЕуЃЌжБЯп
ЩЯЕФЖЏЕуЃЌжБЯп![]() ЃЌ
ЃЌ![]() ЗжБ№НЛЭждВгк
ЗжБ№НЛЭждВгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧѓЫФБпаЮ
СНЕуЃЌЧѓЫФБпаЮ![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтЕУ![]() ЃЌ
ЃЌ![]() ЃЌНсКЯЭМ2ЃЌПЩжЊЭждВ
ЃЌНсКЯЭМ2ЃЌПЩжЊЭждВ![]() ЕФГЄАыжсГЄЮЊ3ЃЌЖЬАыжсГЄЮЊ1ЃЌЙЪПЩЕУЭждВЕФЗНГЬЃЛ
ЕФГЄАыжсГЄЮЊ3ЃЌЖЬАыжсГЄЮЊ1ЃЌЙЪПЩЕУЭждВЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌдђжБЯп
ЃЌдђжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌгЩ
ЃЌгЩ ЕУ
ЕУ![]() ЃЌЫуГі
ЃЌЫуГі![]() ЃЌЭЌРэЕУ
ЃЌЭЌРэЕУ![]() ЃЌЫљвдЕУЫФБпаЮ
ЃЌЫљвдЕУЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ ЃЌСю
ЃЌСю![]() НтЗНГЬЧѓГі
НтЗНГЬЧѓГі![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌгЩЖдГЦадПЩЕУ
ЪБЃЌгЩЖдГЦадПЩЕУ![]() ЃЌЙЪПЩЕУЗћКЯЬѕМўЕФЕу
ЃЌЙЪПЩЕУЗћКЯЬѕМўЕФЕу![]() .
.
ЃЈ1ЃЉгЩЬтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЫљвдЭждВ
ЃЌЫљвдЭждВ![]() ЕФГЄАыжсГЄЮЊ3ЃЌЖЬАыжсГЄЮЊ1ЃЌ
ЕФГЄАыжсГЄЮЊ3ЃЌЖЬАыжсГЄЮЊ1ЃЌ
ЙЪЭждВ![]() ЕФЗНГЬЮЊЃК
ЕФЗНГЬЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌдђжБЯп
ЃЌдђжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() .Щш
.Щш![]() ЃЌ
ЃЌ![]() .
.
гЩ ЃЌЯћ
ЃЌЯћ![]() ЕУ
ЕУ![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌдђ
ЃЌдђ![]() .
.
гЩ ЃЌЯћ
ЃЌЯћ![]() ЕУ
ЕУ![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌдђ
ЃЌдђ![]() .
.
ЫљвдЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ
 .
.
гЩгк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪ .
.
НтЕУ![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌМД
ЃЈЩсШЅЃЉЃЌМД![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌгЩЖдГЦадПЩЕУ
ЪБЃЌгЩЖдГЦадПЩЕУ![]() ЃЌ.
ЃЌ.
злЩЯЃЌЕБЕу![]() Лђ
Лђ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙкзДВЁЖОЪЧвЛИіДѓаЭВЁЖОМвзхЃЌМКжЊПЩв§Ц№ИаУАвдМАжаЖЋКєЮќзлКЯеїЃЈ![]() ЃЉКЭбЯжиМБадКєЮќзлКЯеїЃЈ
ЃЉКЭбЯжиМБадКєЮќзлКЯеїЃЈ![]() ЃЉЕШНЯбЯжиМВВЁ.ЖјНёФъГіЯждкКўББЮфККЕФаТаЭЙкзДВЁЖОЃЈ
ЃЉЕШНЯбЯжиМВВЁ.ЖјНёФъГіЯждкКўББЮфККЕФаТаЭЙкзДВЁЖОЃЈ![]() ЃЉЪЧвдЧАДгЮДдкШЫЬхжаЗЂЯжЕФЙкзДВЁЖОаТЖОжъ.ШЫИаШОСЫаТаЭЙкзДВЁЖОКѓГЃМћЬхеїгаКєЮќЕРжЂзДЁЂЗЂШШЁЂПШЫдЁЂЦјДйКЭКєЮќРЇФбЕШ.дкНЯбЯжиВЁР§жаЃЌИаШОПЩЕМжТЗЮбзЁЂбЯжиМБадКєЮќзлКЯеїЁЂЩіЫЅНпЃЌЩѕжСЫРЭі.
ЃЉЪЧвдЧАДгЮДдкШЫЬхжаЗЂЯжЕФЙкзДВЁЖОаТЖОжъ.ШЫИаШОСЫаТаЭЙкзДВЁЖОКѓГЃМћЬхеїгаКєЮќЕРжЂзДЁЂЗЂШШЁЂПШЫдЁЂЦјДйКЭКєЮќРЇФбЕШ.дкНЯбЯжиВЁР§жаЃЌИаШОПЩЕМжТЗЮбзЁЂбЯжиМБадКєЮќзлКЯеїЁЂЩіЫЅНпЃЌЩѕжСЫРЭі.
ФГвНдКЮЊЩИВщЙкзДВЁЖОЃЌашвЊМьбщбЊвКЪЧЗёЮЊбєадЃЌЯжгаnЃЈ![]() ЃЉЗнбЊвКбљБОЃЌгавдЯТСНжжМьбщЗНЪНЃК
ЃЉЗнбЊвКбљБОЃЌгавдЯТСНжжМьбщЗНЪНЃК
ЗНЪНвЛЃКж№ЗнМьбщЃЌдђашвЊМьбщnДЮ.
ЗНЪНЖўЃКЛьКЯМьбщЃЌНЋЦфжаkЃЈ![]() Чв
Чв![]() ЃЉЗнбЊвКбљБОЗжБ№ШЁбљЛьКЯдквЛЦ№Мьбщ.
ЃЉЗнбЊвКбљБОЗжБ№ШЁбљЛьКЯдквЛЦ№Мьбщ.
ШєМьбщНсЙћЮЊвѕадЃЌетkЗнЕФбЊвКШЋЮЊвѕадЃЌвђЖјетkЗнбЊвКбљБОжЛвЊМьбщвЛДЮОЭЙЛСЫЃЌШчЙћМьбщНсЙћЮЊбєадЃЌЮЊСЫУїШЗетkЗнбЊвКОПОЙФФМИЗнЮЊбєадЃЌОЭвЊЖдетkЗндйж№ЗнМьбщЃЌДЫЪБетkЗнбЊвКЕФМьбщДЮЪ§змЙВЮЊ![]() .
.
МйЩшдкНгЪмМьбщЕФбЊвКбљБОжаЃЌУПЗнбљБОЕФМьбщНсЙћЪЧбєадЛЙЪЧвѕадЖМЪЧЖРСЂЕФЃЌЧвУПЗнбљБОЪЧбєадНсЙћЕФИХТЪЮЊpЃЈ![]() ЃЉ.ЯжШЁЦфжаkЃЈ
ЃЉ.ЯжШЁЦфжаkЃЈ![]() Чв
Чв![]() ЃЉЗнбЊвКбљБОЃЌМЧВЩгУж№ЗнМьбщЗНЪНЃЌбљБОашвЊМьбщЕФзмДЮЪ§ЮЊ
ЃЉЗнбЊвКбљБОЃЌМЧВЩгУж№ЗнМьбщЗНЪНЃЌбљБОашвЊМьбщЕФзмДЮЪ§ЮЊ![]() ЃЌВЩгУЛьКЯМьбщЗНЪНЃЌбљБОашвЊМьбщЕФзмДЮЪ§ЮЊ
ЃЌВЩгУЛьКЯМьбщЗНЪНЃЌбљБОашвЊМьбщЕФзмДЮЪ§ЮЊ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЪдЧѓpЙигкkЕФКЏЪ§ЙиЯЕЪН
ЃЌЪдЧѓpЙигкkЕФКЏЪ§ЙиЯЕЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєpгыИЩШХЫиМЦСП![]() ЯрЙиЃЌЦфжа
ЯрЙиЃЌЦфжа![]() ЃЈ
ЃЈ![]() ЃЉЪЧВЛЭЌЕФе§ЪЕЪ§ЃЌ
ЃЉЪЧВЛЭЌЕФе§ЪЕЪ§ЃЌ
Тњзу![]() Чв
Чв![]() ЃЈ
ЃЈ![]() ЃЉЖМга
ЃЉЖМга![]() ГЩСЂ.
ГЩСЂ.
ЃЈiЃЉЧѓжЄЃКЪ§Са![]() ЕШБШЪ§СаЃЛ
ЕШБШЪ§СаЃЛ
ЃЈiiЃЉЕБ![]() ЪБЃЌВЩгУЛьКЯМьбщЗНЪНПЩвдЪЙЕУбљБОашвЊМьбщЕФзмДЮЪ§ЕФЦкЭћжЕБШж№ЗнМьбщЕФзмДЮЪ§ЕФЦкЭћжЕИќЩйЃЌЧѓkЕФзюДѓжЕ
ЪБЃЌВЩгУЛьКЯМьбщЗНЪНПЩвдЪЙЕУбљБОашвЊМьбщЕФзмДЮЪ§ЕФЦкЭћжЕБШж№ЗнМьбщЕФзмДЮЪ§ЕФЦкЭћжЕИќЩйЃЌЧѓkЕФзюДѓжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌЧвОЙ§Еу
ЃЌЧвОЙ§Еу![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() зїжБЯпНЛЭждВ
зїжБЯпНЛЭждВ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌШєЕу
СНЕуЃЌШєЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕуЮЊ
жсЕФЖдГЦЕуЮЊ![]() ЃЌжЄУїжБЯп
ЃЌжЄУїжБЯп![]() Й§ЖЈЕу.
Й§ЖЈЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧОиаЮ
ЪЧОиаЮ![]() ФкЃЈКЌБпНчЃЉЕФЖЏЕуЃЌЧв
ФкЃЈКЌБпНчЃЉЕФЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЧЮЊ
ЫљГЩЕФНЧЮЊ![]() .МЧЕу
.МЧЕу![]() ЕФЙьМЃГЄЖШЮЊ
ЕФЙьМЃГЄЖШЮЊ![]() ЃЌдђ
ЃЌдђ![]() ______ЃЛЕБШ§РтзЖ
______ЃЛЕБШ§РтзЖ![]() ЕФЬхЛ§зюаЁЪБЃЌШ§РтзЖ
ЕФЬхЛ§зюаЁЪБЃЌШ§РтзЖ![]() ЕФЭтНгЧђЕФБэУцЛ§ЮЊ______.
ЕФЭтНгЧђЕФБэУцЛ§ЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPЉABCDЕФЕзУцABCDЪЧе§ЗНаЮЃЌPAЁЭЕзУцABCDЃЌEЃЌFЗжБ№ЪЧACЃЌPBЕФжаЕуЃЎ
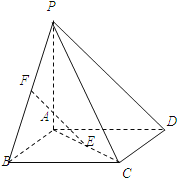
ЃЈ1ЃЉжЄУїЃКEFЁЮЦНУцPCDЃЛ
ЃЈ2ЃЉЧѓжЄЃКУцPBDЁЭУцPACЃЛ
ЃЈ3ЃЉШєPA=ABЃЌЧѓPDгыЦНУцPACЫљГЩНЧЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
![]() .
.
ЃЈ1ЃЉжЄУїЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌЮозюДѓжЕЃЛ
газюаЁжЕЃЌЮозюДѓжЕЃЛ
ЃЈ2ЃЉШєдкЧјМф![]() ЩЯЗНГЬ
ЩЯЗНГЬ![]() ЧЁгавЛИіЪЕЪ§ИљЃЌЧѓ
ЧЁгавЛИіЪЕЪ§ИљЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌвбжЊЕу
жаЃЌвбжЊЕу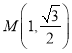 ЃЌ
ЃЌ![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ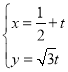 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФЦеЭЈЗНГЬКЭ
ЕФЦеЭЈЗНГЬКЭ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЧњЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГВЭЬќЭЈЙ§ВщдФСЫзюНќ5ДЮЪГЦЗНЛвзЛсВЮЛсШЫЪ§![]() (ЭђШЫ)гыВЭЬќЫљгУдВФСЯЪ§СП
(ЭђШЫ)гыВЭЬќЫљгУдВФСЯЪ§СП![]() (Дќ)ЃЌЕУЕНШчЯТЭГМЦБэЃК
(Дќ)ЃЌЕУЕНШчЯТЭГМЦБэЃК
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ | ЕкЮхДЮ | |
ВЮЛсШЫЪ§ | 13 | 9 | 8 | 10 | 12 |
дВФСЯ | 32 | 23 | 18 | 24 | 28 |
ЃЈ1ЃЉИљОнЫљИј5зщЪ§ОнЃЌЧѓГі![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]() .
.
ЃЈ2ЃЉвбжЊЙКТђдВФСЯЕФЗбгУ![]() (дЊ)гыЪ§СП
(дЊ)гыЪ§СП![]() (Дќ)ЕФЙиЯЕЮЊ
(Дќ)ЕФЙиЯЕЮЊ![]() ЃЌ
ЃЌ
ЭЖШыЪЙгУЕФУПДќдВФСЯЯргІЕФЯњЪлЪеШыЮЊ700дЊЃЌЖргрЕФдВФСЯжЛФмЮоГЅЗЕЛЙЃЌОнЯЄБОДЮНЛвзДѓЛсДѓдМга15ЭђШЫВЮМгЃЌИљОн(1)жаЧѓГіЕФЯпадЛиЙщЗНГЬЃЌдЄВтВЭЬќгІЙКТђЖрЩйДќдВФСЯЃЌВХФмЛёЕУзюДѓРћШѓЃЌзюДѓРћШѓЪЧЖрЩйЃП(зЂЃКРћШѓ![]() ЯњЪлЪеШы
ЯњЪлЪеШы![]() дВФСЯЗбгУ).
дВФСЯЗбгУ).
ВЮПМЙЋЪНЃК  ЃЌ
ЃЌ ![]() .
.
ВЮПМЪ§ОнЃК ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧОиаЮЃЌВрРт
ЪЧОиаЮЃЌВрРт![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
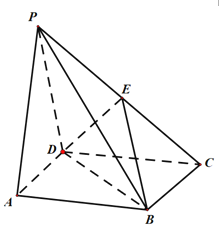
![]() ЧѓжЄЃК
ЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
![]() ШєжБЯп
ШєжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЮЊ
ЫљГЩНЧЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФДѓаЁ.
ЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com