
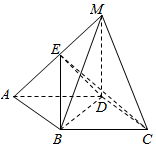
分析 (1)根据线面垂直的性质定理证明DE⊥平面MAB即可.
(2)取AD的中点H,连接EH,EH是三棱锥E-ABD的高,根据割补法得到三棱锥M-EBC的体积VM-EBC=VM-ABCD-VE-ABD,分别根据三棱锥的体积公式进行求解即可.
解答 (1)证明:∵MD=DA=1,E为MA中点,
∴DE⊥MA,
∵MD⊥平面ABCD,MD?平面MAD,
∴平面MAD⊥平面ABCD,
∵底面ABCD为矩形,∴AB⊥平面MAD,
∵DE?平面MAD,
∴AB⊥DE,
∵MA∩AB=A,
∴DE⊥平面MAB,
∵MB?平面MAB,
∴DE⊥MB
(2)取AD的中点H,连接EH,则EH∥DM,且EH=$\frac{1}{2}$MD=$\frac{1}{2}$,
则EH⊥平面ABCD,
即EH是三棱锥E-ABD的高,
若DC=2,则S△ABD=$\frac{1}{2}$AB•AD=$\frac{1}{2}$×1×2=1,SABCD=AB•AD=1×2=2,
则VE-ABD=$\frac{1}{3}$S△ABD•EH=$\frac{1}{3}$×1×$\frac{1}{2}$=$\frac{1}{6}$,VM-ABCD=$\frac{1}{3}$SABCD•MD=$\frac{1}{3}×$2×1=$\frac{2}{3}$,
则三棱锥M-EBC的体积VM-EBC=VM-ABCD-VE-ABD=$\frac{2}{3}$-$\frac{1}{6}$=$\frac{1}{2}$.
点评 本题主要考查看空间直线垂直的判定以及三棱锥的体积的计算,根据割补法将三棱锥M-EBC的体积转化为两个规则三棱锥的体积差是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学平均名次 物理平均名次 | 1.3 2.3 | 12.3 9.7 | 25.7 31.0 | 36.7 22.3 | 50.3 40.0 | 67.7 58.0 | 49.0 39.0 | 52.0 60.7 | 40.0 63.3 | 34.3 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学平均名次 物理平均名次 | 78.3 49.7 | 50.0 46.7 | 65.7 83.3 | 66.3 59.7 | 68.0 50.0 | 95.0 101.3 | 90.7 76.7 | 87.7 86.0 | 103.7 99.7 | 86.7 99.0 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 2 | 12 | 23 | 18 | 10 | x |
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 5 | 12 | 18 | 10 | 3 | y |
| 运动达人 | 非运动达人 | 总 计 | |
| 男 生 | |||
| 女 生 | |||
| 总 计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com