
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 2 | 12 | 23 | 18 | 10 | x |
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 5 | 12 | 18 | 10 | 3 | y |
| 运动达人 | 非运动达人 | 总 计 | |
| 男 生 | |||
| 女 生 | |||
| 总 计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)由分层抽样求出男生抽取的人数,女生抽取人数,然后求解该校男生平均每天运动的时间.
(Ⅱ)①样本中“运动达人”所占比例是$\frac{20}{120}=\frac{1}{6}$,故估计该校“运动达人”人数;②填写表格,求解K2的观测值,推出在犯错误的概率不超过0.05的前提下,‘运动达人’与性别有关”的结果.
解答 解:(Ⅰ)由分层抽样得:男生抽取的人数为$120×\frac{14000}{14000+10000}=70$人,女生抽取人数为120-70=50人,故x=5,y=2,(2分)
则该校男生平均每天运动的时间为:$\frac{0.25×2+0.75×12+1.25×23+1.75×18+2.25×10+2.75×5}{70}≈1.5$,(5分)
故该校男生平均每天运动的时间约为1.5小时;
(Ⅱ)①样本中“运动达人”所占比例是$\frac{20}{120}=\frac{1}{6}$,故估计该校“运动达人”有$\frac{1}{6}×({14000+10000})=4000$人; (8分)
②由表格可知:
| 运动达人 | 非运动达人 | 总 计 | |
| 男 生 | 15 | 55 | 70 |
| 女 生 | 5 | 45 | 50 |
| 总 计 | 20 | 100 | 120 |
点评 本题考查分层抽样,独立检验的思想方法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业量大 | 认为作业量不大 | 总计 | |
| 男生 | 18 | 9 | 27 |
| 女生 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
| P(χ2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 99% | B. | 95% | C. | 90% | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
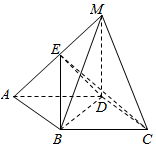
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{π}{4}$) | B. | (1,$\frac{3π}{4}$) | C. | (1,$\frac{5π}{4}$) | D. | (1,$\frac{7π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
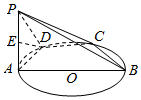 如图,已知等腰梯形ABCD为⊙O的内接四边形,AB∥CD,PA=AB=2CD=2,PA⊥平面ABCD,已知E为PA的中点,连接DE.
如图,已知等腰梯形ABCD为⊙O的内接四边形,AB∥CD,PA=AB=2CD=2,PA⊥平面ABCD,已知E为PA的中点,连接DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com