

| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2013}{2014}$ |
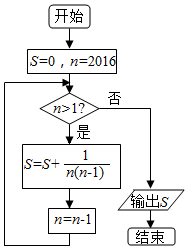
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2016×2017}$的值,用裂项法即可计算求值得解.
解答 解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是累加并输出S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2016×2017}$的值.
而S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
故选:C.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
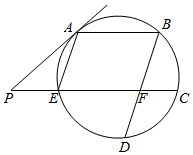 如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.
如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学平均名次 物理平均名次 | 1.3 2.3 | 12.3 9.7 | 25.7 31.0 | 36.7 22.3 | 50.3 40.0 | 67.7 58.0 | 49.0 39.0 | 52.0 60.7 | 40.0 63.3 | 34.3 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学平均名次 物理平均名次 | 78.3 49.7 | 50.0 46.7 | 65.7 83.3 | 66.3 59.7 | 68.0 50.0 | 95.0 101.3 | 90.7 76.7 | 87.7 86.0 | 103.7 99.7 | 86.7 99.0 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{1}{2015}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 2 | 12 | 23 | 18 | 10 | x |
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 5 | 12 | 18 | 10 | 3 | y |
| 运动达人 | 非运动达人 | 总 计 | |
| 男 生 | |||
| 女 生 | |||
| 总 计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com