
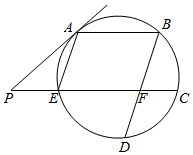
 如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.
如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.分析 (1)利用△PAE∽△EB A,及切割线定理求AE的长;
(2)利用相交弦定理证明BF=FD,即可证明点F是 BD的中点.
解答 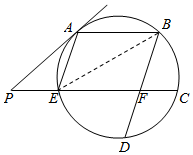 (1)解:∵PA2=PC•P E,PA=2,PE=1,∴PC=4,(2分)
(1)解:∵PA2=PC•P E,PA=2,PE=1,∴PC=4,(2分)
又∵P E=CF=1,∴EF=2,
∵∠PA E=∠EB A,∠PE A=∠EA B,
∴△PAE∽△EB A,∴$\frac{{{P}{E}}}{{{A}{E}}}=\frac{{{A}{E}}}{{{A}{B}}}$,(4分)
∴AE2=P E•A B=2,∴${A}{E}=\sqrt{2}$.(5分)
(2)证明:∵${B}F={A}{E}=\sqrt{2}$,EF=2,而 EF•FC=BF•FD,(8分)
∴$DF=\frac{2•1}{{\sqrt{2}}}=\sqrt{2}$,∴BF=FD,
∴点F是 BD的中点.(10分)
点评 本题考查切割线定理、相交弦定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.04 | B. | 0.64 | C. | 0.86 | D. | 0.96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业量大 | 认为作业量不大 | 总计 | |
| 男生 | 18 | 9 | 27 |
| 女生 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
| P(χ2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 99% | B. | 95% | C. | 90% | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com