
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 由已知条件a+b+c=0,a2+b2+c2=1,变形后,得到bc与b+c的值,利用完全平方式将变形后的式子代入推出b、c是二次方程的两个实数根,利用根的判别式得到有关a的不等式后确定a的取值范围.
解答 解:∵a+b+c=0,a2+b2+c2=1,
∴b+c=-a,b2+c2=1-a2,
∴bc=$\frac{1}{2}$•(2bc)
=$\frac{1}{2}$[(b+c)2-(b2+c2)]
=a2-$\frac{1}{2}$
∴b、c是方程:x2+ax+a2-$\frac{1}{2}$=0的两个实数根,
∴△≥0
∴a2-4(a2-$\frac{1}{2}$)≥0
即a2≤$\frac{2}{3}$
∴-$\frac{\sqrt{6}}{3}$≤a≤$\frac{\sqrt{6}}{3}$
即a的最大值为$\frac{\sqrt{6}}{3}$
故选:B.
点评 本题考查了函数最值问题,函数与方程的综合应用,解决本题的关键是利用根的判别式得到有关未知数的不等式,进而求得a的取值范围.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 男性公务员 | 女性公务员 总计 | ||
| 生二胎 | |||
| 不生二胎 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)是偶函数且有最大值 | B. | 函数f(x)是偶函数且有最小值 | ||
| C. | 函数f(x)是奇函数且有最大值 | D. | 函数f(x)是奇函数且有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
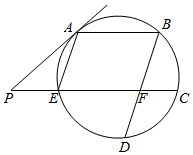 如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.
如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com