
分析 先求出函数的解析式,再代入计算,即可得出结论.
解答 解:由题意,-f(x)+g(x)=e-x,
与条件联立可得,f(x)=$\frac{1}{2}$(ex-e-x),g(x)=$\frac{1}{2}$(ex+e-x),
∴$\frac{{2}^{n}g(1)g(2)g({2}^{2})…g({2}^{n-1})}{f({2}^{n})}$=$\frac{(e+{e}^{-1})({e}^{2}+{e}^{-2})…({e}^{{2}^{n-1}}+{e}^{-{2}^{n-1}})}{\frac{1}{2}({e}^{{2}^{n}}-{e}^{-{2}^{n}})}$=$\frac{2}{e+{e}^{-1}}$=$\frac{2e}{{e}^{2}+1}$.
故答案为:$\frac{2e}{{e}^{2}+1}$.
点评 本题考查函数的奇偶性,考查函数解析式的求解,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
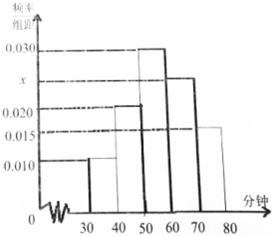 4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”
4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”| 非读书迷 | 读书迷 | 合计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
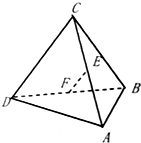 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=4,CD=2,EF⊥AB,则EF与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=4,CD=2,EF⊥AB,则EF与CD所成角的度数为( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{{42}^5}}}$ | B. | $\frac{1}{{{{42}^4}}}$ | C. | $\frac{{A}_{42}^{5}}{4{2}^{5}}$ | D. | $\frac{{P_{42}^4}}{{{{42}^5}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com