
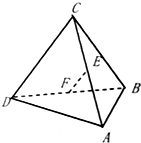
 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=4,CD=2,EF⊥AB,则EF与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=4,CD=2,EF⊥AB,则EF与CD所成角的度数为( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |
分析 设G为AD的中点,连接GF,GE,则GE,GF分别为△ACD,△ABD的中位线.由此可得GF∥AB,GE∥CD,可得∠FEG或其补角即为EF与CD所成角.再利用三角形中位线定理、直角三角形的边角关系即可得出.
解答 解:设G为AD的中点,连接GF,GE,则GE,GF分别为△ACD,△ABD的中位线.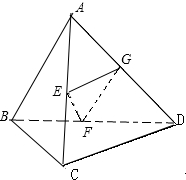
由此可得GF∥AB,且GF=$\frac{1}{2}$AB=1.GE∥CD,且GE=$\frac{1}{2}$CD=2.
∴∠FEG或其补角即为EF与CD所成角.又∵EF⊥AB,GF∥AB,∴EF⊥GF.
因此,Rt△EFG中,可得sin∠GEF=$\frac{GF}{GE}$=$\frac{1}{2}$,可得∠GEF=30°.
∴EF与CD所成的角的度数为30°.
故选:D.
点评 本题考查了异面直线所成的角、三角形中位线定理、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 男性公务员 | 女性公务员 总计 | ||
| 生二胎 | |||
| 不生二胎 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)是偶函数且有最大值 | B. | 函数f(x)是偶函数且有最小值 | ||
| C. | 函数f(x)是奇函数且有最大值 | D. | 函数f(x)是奇函数且有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com