练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．投篮测试中，每人投3次，至少投中2次才能通过测试．已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为$\frac{81}{125}$．

    分析 分类讨论，利用n次独立重复试验中恰好发生k次的概率公式，计算求得结果．

    解答 解：该同学通过测试的概率为${C}_{3}^{2}$•0.62•0.4+${C}_{3}^{3}$•0.63=$\frac{81}{125}$，
    故答案为：$\frac{81}{125}$．

    点评 本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式，解答本题关键是判断出所研究的事件是那一种概率模型，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知曲线C1：x+$\sqrt{3}$y=$\sqrt{3}$和C2：$\left\{\begin{array}{l}{x=\sqrt{6}cosφ}\\{y=\sqrt{2}sinφ}\end{array}\right.$（φ为参数），以原点O为极点，x 轴的正半轴为极轴，建立极坐标系，且两种坐标系中取相同的长度单位．
    （1）把曲线C1、C2的方程化为极坐标方程
    （2）设C1与x轴、y轴交于M，N两点，且线段MN的中点为P．若射线OP与C1、C2交于P、Q两点，求P，Q两点间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=\sqrt{3}sinα}\end{array}\right.$，（α为参数），以坐标原点为极点，以x轴的非负半轴为极轴建立极坐标系，点A的极坐标为（2$\sqrt{2}$，$\frac{π}{4}$）．
    （1）写出曲线C的极坐标方程，并求出曲线C在点（$\sqrt{2}$，1）处的切线l的极坐标方程；
    （2）若过点A的直线m与曲线C相切，求直线m的斜率k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图所示，已知SA⊥正方形ABCD所在平面，O为AC与BD的交点．
    （1）求证：平面SBC⊥平面SAB；
    （2）求二面角B-SA-C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．如图，在直角△ABC中，AB⊥BC，D为BC的中点，以AB为直径作圆O，分别交AC、AD于点E，F，若AF=3，FD=1，则AE等于（　　）
    A．$\sqrt{6}$B．$\frac{6\sqrt{7}}{7}$C．$\frac{8\sqrt{7}}{7}$D．$\frac{4\sqrt{21}}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知P={f（x）|存在正实数M，使得对定义域中的一切x都有|f（x）|≤M成立}，h（x）=2x-$\sqrt{1-x}$，x∈[0，1]，g（x）=$\sqrt{x-3}$-$\sqrt{x+2}$，则（　　）
    A．g（x）∉P，h（x）∈PB．g（x）∈P，h（x）∈PC．g（x）⊆P，h（x）⊆PD．g（x）∈P，h（x）∉P

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

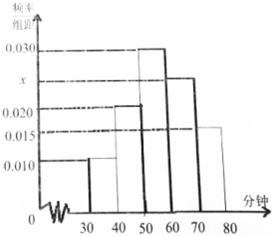    18．4月23日是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”
    （Ⅰ）求x的值并估计该校3000名学生中读书谜大概有多少？（将频率视为概率）
    （Ⅱ）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？
    非读书迷读书迷合计
    男 15 
    女  45
    合计  
    （Ⅲ）根据（Ⅱ）的结论，能否提出更好的调查方法来估计该地区的学生的课外阅读时间？说明理由．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d
    P（K2≥k0）0.1000.0500.0250.0100.001
    k02.7063.8415.0246.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

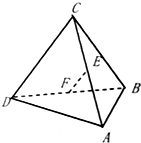    15．已知四面体ABCD中，E，F分别是AC，BD的中点，若AB=4，CD=2，EF⊥AB，则EF与CD所成角的度数为（　　）
    A．90°B．45°C．60°D．30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．正方体ABCD-A1B1C1D1，E，F分别是上底面A1B1C1D1和侧面CDD1C1的中心，若$\overrightarrow{AF}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AE}$，则x+y+z=$\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案