
分析 运用基本不等式可得f(x)≥2$\sqrt{k}$,由等号成立的条件可得$\sqrt{k}$∈[1,3],继而求出k的最大值与最小值.
解答 解:由题意得:x>0,
∴f(x)=x+$\frac{k}{x}$≥2$\sqrt{k}$,
∵函数f(x)=x+$\frac{k}{x}$在[1,3]上的最小值为2$\sqrt{k}$,
当x=$\sqrt{k}$时,函数f(x)取得最小值2$\sqrt{k}$,
∴$\sqrt{k}$∈[1,3],
∴k的最小值为1,最大值为9.
∴正数k的最大值与最小值之和为10.
故答案为:10.
点评 本题考查了基本不等式的运用:求最值,考查了运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
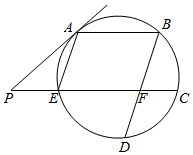 如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.
如图,A、B、C、D、E在圆周上,且 A B∥C E,A E∥BD,BD交C E于点F,过 A点的圆的切线交C E的延长线于 P,若 PE=CF=1,P A=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学平均名次 物理平均名次 | 1.3 2.3 | 12.3 9.7 | 25.7 31.0 | 36.7 22.3 | 50.3 40.0 | 67.7 58.0 | 49.0 39.0 | 52.0 60.7 | 40.0 63.3 | 34.3 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学平均名次 物理平均名次 | 78.3 49.7 | 50.0 46.7 | 65.7 83.3 | 66.3 59.7 | 68.0 50.0 | 95.0 101.3 | 90.7 76.7 | 87.7 86.0 | 103.7 99.7 | 86.7 99.0 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
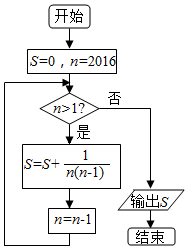
| A. | $\frac{1}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{1}{2015}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com