练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知抛物线C：y2=x的焦点为F，A（x0，y0）是C上一点，若|AF|=$\frac{5}{4}$x0，则x0等于（　　）
    A．1B．2C．4D．8

    分析 利用抛物线的定义、焦点弦长公式即可得出．

    解答 解：抛物线C：y2=x的焦点为F（$\frac{1}{4}$，0）
    ∵A（x0，y0）是C上一点，|AF|=$\frac{5}{4}$x0，
    ∴$\frac{5}{4}$x0=x0+$\frac{1}{4}$，
    解得x0=1．
    故选：A．

    点评 本题考查了抛物线的定义、焦点弦长公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

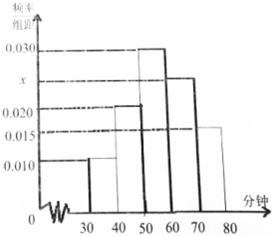    18．4月23日是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，并用简单随机抽样方法抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”
    （Ⅰ）求x的值并估计该校3000名学生中读书谜大概有多少？（将频率视为概率）
    （Ⅱ）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？
    非读书迷读书迷合计
    男 15 
    女  45
    合计  
    （Ⅲ）根据（Ⅱ）的结论，能否提出更好的调查方法来估计该地区的学生的课外阅读时间？说明理由．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d
    P（K2≥k0）0.1000.0500.0250.0100.001
    k02.7063.8415.0246.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某校某班级有42人，该班委会决定每月第一周的周一抽签决定座位，该班级座位排成6列7行，同学先在写有1、2、3、4、5、6的卡片中任取一张，确定所在列，再在写有1、2、3、4、5、6、7的卡片中任取一张确定所在行，如先后抽到卡片为2、5，则此同学座位为第2列第5行，在一学期的5次抽签中，该班班长5次位置均不相同的概率是（　　）
    A．$\frac{1}{{{{42}^5}}}$B．$\frac{1}{{{{42}^4}}}$C．$\frac{{A}_{42}^{5}}{4{2}^{5}}$D．$\frac{{P_{42}^4}}{{{{42}^5}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．正方体ABCD-A1B1C1D1，E，F分别是上底面A1B1C1D1和侧面CDD1C1的中心，若$\overrightarrow{AF}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AE}$，则x+y+z=$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．不等式$\frac{{{x^2}-1}}{2x-1}$≤0的解集是$（{-∞，-1}]∪（{\frac{1}{2}，1}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．点C是线段AB的中点，$\overrightarrow{AB}$=λ$\overrightarrow{AC}$，那么λ等于（　　）
    A．-2B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．参数方程$\left\{\begin{array}{l}{x=\sqrt{{t}^{2}+2t+3}}\\{y=\sqrt{{t}^{2}+2t+2}}\end{array}\right.$（t为参数）表示的曲线是（　　）
    A．双曲线x2-y2=1B．双曲线x2-y2=1的右支
    C．双曲线x2-y2=1且x≥0，y≥0D．以上结论都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若函数f（x）=x+$\frac{k}{x}$在[1，3]上的最小值为2$\sqrt{k}$，则正数k的最大值与最小值之和为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知随机变量ξ服从正态分布 N（2，1），P（ξ≤3）=0.8413，则 P（ξ≤1）=0.1587．

    查看答案和解析>>

    同步练习册答案