
| A. | (1,$\frac{π}{4}$) | B. | (1,$\frac{3π}{4}$) | C. | (1,$\frac{5π}{4}$) | D. | (1,$\frac{7π}{4}$) |
分析 ρ=2cos($θ+\frac{π}{4}$)即ρ2=2ρcos($θ+\frac{π}{4}$),展开为ρ2=2ρ×$\frac{\sqrt{2}}{2}$(cosθ-sinθ),把ρ2=x2+y2,x=ρcosθ,y=ρsinθ,化为直角坐标方程,可得圆心的直角坐标,进而化为极坐标.
解答 解:ρ=2cos($θ+\frac{π}{4}$)即ρ2=2ρcos($θ+\frac{π}{4}$),
展开为ρ2=2ρ×$\frac{\sqrt{2}}{2}$(cosθ-sinθ),化为直角坐标方程:x2+y2=$\sqrt{2}$(x-y),
∴$(x-\frac{\sqrt{2}}{2})^{2}$+$(y+\frac{\sqrt{2}}{2})^{2}$=1,
可得圆心为C$(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$,可得$ρ=\sqrt{(\frac{\sqrt{2}}{2})^{2}+(-\frac{\sqrt{2}}{2})^{2}}$=1,
tanθ=-1,又点C在第四象限,θ=$\frac{7π}{4}$.
∴圆心C$(1,\frac{7π}{4})$.
故选:D.
点评 本题考查了极坐标化为直角坐标、三角函数求值,考查了推理能力与计算能力,属于中档题.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
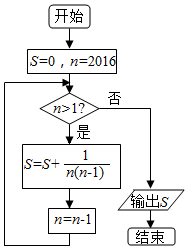
| A. | $\frac{1}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{1}{2015}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 2 | 12 | 23 | 18 | 10 | x |
| 平均每天运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 5 | 12 | 18 | 10 | 3 | y |
| 运动达人 | 非运动达人 | 总 计 | |
| 男 生 | |||
| 女 生 | |||
| 总 计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
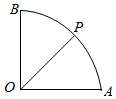 扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )
扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [1,$\sqrt{3}$] | C. | [1,2] | D. | [1,$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
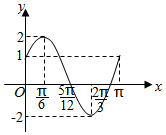 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com