
已知曲线C上的动点P(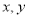 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线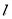 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。
(1)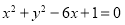 (或
(或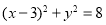 )(2)
)(2) 或
或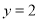 .
.
【解析】
试题分析:(1)根据动点P(x,y)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为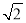 ,建立方程,化简可得曲线C的方程.
,建立方程,化简可得曲线C的方程.
(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线l的方程.
试题解析:(1)由题意得|PA|=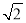 |PB| 2分;
|PB| 2分;
故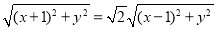 3分;
3分;
化简得: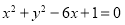 (或
(或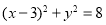 )即为所求。 5分;
)即为所求。 5分;
(2)当直线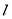 的斜率不存在时,直线
的斜率不存在时,直线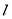 的方程为
的方程为 ,
,
将 代入方程
代入方程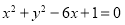 得
得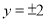 ,所以|MN|=4,满足题意。 8分;
,所以|MN|=4,满足题意。 8分;
当直线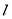 的斜率存在时,设直线
的斜率存在时,设直线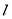 的方程为
的方程为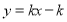 +2
+2
由圆心到直线的距离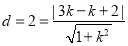 10分;
10分;
解得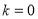 ,此时直线
,此时直线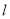 的方程为
的方程为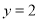
综上所述,满足题意的直线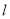 的方程为:
的方程为: 或
或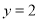 。 12分.
。 12分.
考点:直线和圆的方程的应用.


科目:高中数学 来源:2015届浙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则 等于 ( )
等于 ( )
A. B.
B. C.
C. D .
D .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期第一次统练理科数学试卷(解析版) 题型:选择题
F1,F2是双曲线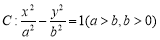 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.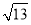 B.
B.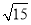 C.2 D.
C.2 D.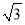
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期第一次统练文科数学试卷(解析版) 题型:选择题
已知抛物线 与直线
与直线 相交于A、B两点,其中A点的坐标是(1,2)。如果抛物线的焦点为F,那么
相交于A、B两点,其中A点的坐标是(1,2)。如果抛物线的焦点为F,那么 等于( )
等于( )
A. 5 B.6 C. 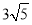 D.7
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com