考点:数列与不等式的综合,等差数列的通项公式,数列的求和
专题:综合题
分析:(1)当n=1时,
a1=S1=a1(a1+1),得a
1=1.当n≥2时,a
n=S
n-S
n-1=
an(an+1)-an-1(an-1+1),得(a
n+a
n-1)(a
n-a
n-1-1)=0,由此能求出a
n=n.
(2)由数列{b
n}满足
b1=1,bn+1=bn+3an,知
bn+1-bn=3an=3n,由此利用累加法能够求出数列{b
n}的通项公式.
(3)由
cn==
,知
Tn=+++…+,由此利用错位相减法能够求出T
n,进而证明
Tn<.
解答:
解:(1)当n=1时,
a1=S1=a1(a1+1),
∴
a12=a1,
∵a
1>0,∴a
1=1.
当n≥2时,a
n=S
n-S
n-1=
an(an+1)-an-1(an-1+1),
化简,得(a
n+a
n-1)(a
n-a
n-1-1)=0,
∵a
n>0,∴a
n-a
n-1=1,
故数列{a
n}是以1为首项,1为公差的等差数列,
∴a
n=n.
(2)∵数列{b
n}满足
b1=1,bn+1=bn+3an,
∴
bn+1-bn=3an=3n,
∴b
n=b
1+(b
2-b
1)+(b
3-b
2)+…+(b
n-b
n-1)
=1+3+3
2+…+3
n-1=
=
(3n-1).
(3)∵
cn==
,
∴
Tn=+++…+,
∴
Tn=+++…+,
则
Tn-Tn=+++…+-=
-=
-,
∴
Tn=-<.
点评:本题考查数列通项公式的求法和前n项和的证明,解题时要认真审题,注意累加法、裂项求和法的灵活运用.



 阅读快车系列答案
阅读快车系列答案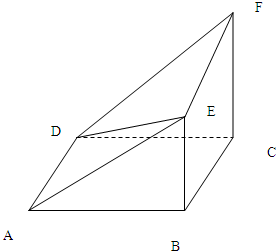 多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.
多面体EF-ABCD中,ABCD为正方形,BE⊥平面ABCD,CF⊥平面ABCD,AB=CF=2BE.