
分析 根据题意作出图形,欲求球O的表面积,只须求球的半径r.利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答 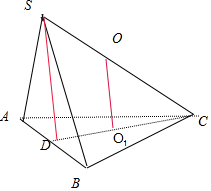 设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
作SD⊥平面ABC交CO1的延长线与D.$\frac{2}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$,∴OO1=$\sqrt{{R}^{2}-\frac{1}{3}}$,
∴高SD=2OO1,
∵△ABC是边长为1的正三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$,∴V三棱锥S-ABC=$\frac{1}{3}×2\sqrt{{R}^{2}-\frac{1}{3}}×\frac{\sqrt{3}}{4}=\frac{\sqrt{2}}{6}$,
∴R=1.则球O的表面积为4π,
故答案为:4π.
点评 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点S到面ABC的距离,属于中档题


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
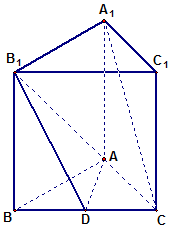 如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.
如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
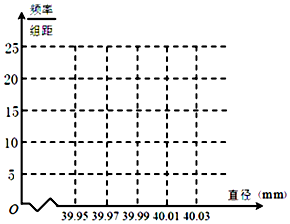 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com