
分析 (Ⅰ)先利用正弦定理把a和b的表达式代入acosB+bcosA中,利用了两角和公式化简整理,求得acosB+bcosA=2RsinC,进而把2RsinC转化成边,原式得证.
(Ⅱ)利用正弦定理化简已知等式,利用两角和与差的正弦函数公式及诱导公式化简,根据sinC不为0求出cosA的值,即可确定出A的度数,进而利用三角形面积公式即可计算得解.
解答 解:(Ⅰ)证明:∵由正弦定理得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
∴左=acosB+bcosA=2RsinAcosB+2RsinBcosA=2Rsin(B+A)=2RsinC=c=右,
原式得证.
(Ⅱ)由(2c-b)cosA=acosB及正弦定理得(2sinC-sinB)cosA=sinAcosB,
得2sinCcosA=sinAcosB+cosAsinB=sin(A+B),
∵A+B+C=π,
∴sin(A+B)=sinC≠0,
∴cosA=$\frac{1}{2}$,
∵A为三角形的内角,
∴A=$\frac{π}{3}$.
∵b=1,c=2,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×1×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了正弦定理,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
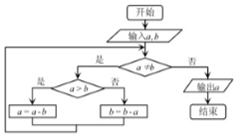 如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为8,18,则输出的a等于( )
如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为8,18,则输出的a等于( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,给出以下四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图(Ⅰ)是反映某条公共汽车线路收支差额y与乘客量x之间关系的图象,由于目前该条公交线路亏损,公司有关人员提出两种调整建议,如图(Ⅱ)(Ⅲ)所示(注:收支差额=营业所得的票价收入-付出的成本)
如图(Ⅰ)是反映某条公共汽车线路收支差额y与乘客量x之间关系的图象,由于目前该条公交线路亏损,公司有关人员提出两种调整建议,如图(Ⅱ)(Ⅲ)所示(注:收支差额=营业所得的票价收入-付出的成本)| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com